下列函数在区间[0,3]上不满足拉格朗日定理条件的是( )《》( )
下列函数在区间[0,3]上不满足拉格朗日定理条件的是( )《》( )
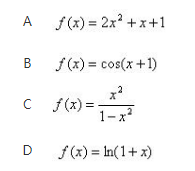
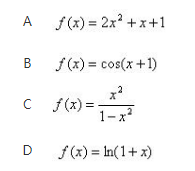
参考解析
解析:
相关考题:
为了保证插值函数能更好地密合原来的函数,不但要求“过点”,即两者在节点上具有相同的函数值,而且要求“相切”,即在节点上还具有相同的导数值,这类插值称为()A、牛顿插值B、埃尔米特插值C、分段插值D、拉格朗日插值
罗尔定理:设函数(x)满足条件:(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;(3)(a)=(b),则在(a,b)内至少存在一点ξ,使得,′(ξ)=0。证明这个定理并说明其几何意义。
研究流体运动的两种方法应该是()。A、拉格朗日法和欧拉法均以质点为研究对象B、拉格朗日法和欧拉法均以固定空间为研究对象C、拉格朗日法以质点为研究对象,而欧拉法以固定空间为研究对象D、拉格朗日法以固定空间为研究对象,而欧拉法以质点为研究对象
单选题研究流体运动的两种方法应该是()。A拉格朗日法和欧拉法均以质点为研究对象B拉格朗日法和欧拉法均以固定空间为研究对象C拉格朗日法以质点为研究对象,而欧拉法以固定空间为研究对象D拉格朗日法以固定空间为研究对象,而欧拉法以质点为研究对象
单选题下列说法正确的是:A分析流体运动时,拉格朗日法比欧拉法在做数学分析时更为简便B拉格朗日法着眼于流体中各个质点的流动情况,而欧拉法着眼于流体经过空间各固定点时的运动情况C流线是拉格朗日法对流动的描述,迹线是欧拉法对流动的描述D拉格朗日法和欧拉法在研究流体运动时,有本质的区别
单选题下列哪个定理与沟通无关()A斯坦纳定理B拉格朗日定理C费斯诺定理D避雷针效应