设三次多项式函数则f(x)的极大值点为( )A.0B.1C.-1D.2
设三次多项式函数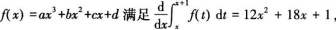
则f(x)的极大值点为( )
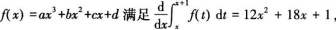则f(x)的极大值点为( )
A.0
B.1
C.-1
D.2
B.1
C.-1
D.2
参考解析
解析：
相关考题：
设函数f(x)在内连续，其导函数的图形如图所示，则f(x)有(52)。A．一个极小值点和两个极大值点B．两个极小值点和一个极大值点C．两个极小值点和两个极大值点D．三个极小值点和一个极大值点
设函数f(x)在x=a的某个邻域内连续，且f(a)为其极大值，则存在δ＞0，当x∈(a-δ，a+δ)时，必有( )。A.(x-a)[f(x)-f(a)]≥0B.(x-a)[f(x)-f(a)]≤0C.D.
f（x）在（－∞，＋∞）内连续，其导数函数f′（x）图形如图所示，则f（x）有（ ）。A．一个极小值点和两个极大值点B．两个极小值点和两个极大值点C．两个极小值点和一个极大值点D．一个极小值点和三个极大值点
下列命题中，正确的是( ).A.单调函数的导函数必定为单调函数B.设f(x)为单调函数，则f(x)也为单调函数C.设f(x)在(a，b)内只有一个驻点xo，则此xo必为f(x)的极值点D.设f(x)在(a，b)内可导且只有一个极值点xo，f(xo)=0
设函数y-f(x)连续，除x=a外f''(x)均存在。一一阶导函数y'=f(x)的图形如下，则y=f(x)A.有两个极大值点，一个极小值点，一个拐点B.有一个极大值点，一个极小值点，两个拐点C.有一个极大值点，一个极小值点，一个拐点D.有一个极大值点，两个极小值点，两个拐点
设函数y=f（x）的导函数，满足f′（一1）=0，当x＜-l时，f′（x）＜0；当x＞-l时，f′（x）＞0.则下列结论肯定正确的是（ ）.《》（ ）A.x=-1是驻点，但不是极值点B.x=-1不是驻点C.x=-1为极小值点D.x=-1为极大值点
单选题设函数f（x）满足关系式f″（x）＋[f′（x）]2＝x，且f′（0）＝0，则（ ）。Af（0）是f（x）的极大值Bf（0）是f（x）的极小值C点（0，f（0））是曲线y＝f（x）的拐点Df（0）不是f（x）的极值，点（0，f（0））也不是曲线y＝f（x）的拐点
单选题设f（x）在x＝0处满足f′（0）＝f″（0）＝…＝f（n）（0），f（n＋1）（0）＞0，则（ ）。A当n为偶数时，x＝0是f（x）的极大值点B当n为偶数时，x＝0是f（x）的极小值点C当n为奇数时，x＝0是f（x）的极大值点D当n为奇数时，x＝0是f（x）的极小值点
单选题设函数z＝f（x，y）的全微分为dz＝xdx＋ydy，则点（0，0）（ ）。A不是f（x，y）的连续点B不是f（x，y）的极值点C是f（x，y）的极大值点D是f（x，y）的极小值点