吉林省名校2019届高三第一次联合模拟考试数学(理)试题Word版含答案
B.√2
C.2
D.1
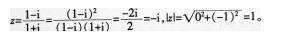
 ,故
,故 .
.
 ,故
,故 .
.
B.{1,2,3}
C.{1,2}
D.{0,4}
B.{0,2}
C.{0,1}
D.{0,1,2}
吉林省名校2019届高三下学期第一次联合模拟考试高三数学考试理科第卷一、选择题:1已知集合A0,1,2,3,BxNlnxx1),则ABA0,1 B1,2 C0,1,2 D0,1,2,32设复数z满足,则|z|A1 B C3 D3已知双曲线(a0,b0)的一条渐近线经过点,则该双曲线的离心率为A2 B C3 D4某机构对青年观众是否喜欢跨年晚会进行了调查,人数如下表所示:不喜欢喜欢男性青年观众3010女性青年观众3050现要在所有参与调查的人中用分层抽样的方法抽取n人做进一步的调研,若在“不喜欢的男性青年观众”的人中抽取了6人,则nA12 B16 C24 D325在ABC中,若点D满足,点E为AC的中点,则A B C D6若某程序框图如图所示,则该程序运行后输出的BA4 B13 C40 D417将函数f(x)sinx的图象向右平移个单位长度后得到函数yg(x)的图象,则函数yf(x)g(x)的最大值为A B C1 D8某几何体的三视图如图所示,则该几何体的体积为A B C D9在ABC中,角A,B,C的对边分别为a,b,c,若b1,点D是边BC的中点,且,则ABC的面积为A B C或 D或10函数f(x)xsin2xcosx的大致图象有可能是ABCD11已知四棱锥SABCD,SA平面ABCD,ABBC,BCDDAB,SA2,二面角SBCA的大小为若四面体SACD的四个顶点都在同一球面上,则该球的表面积为A B4 C8 D1612已知函数f(x)exex,若对任意的x(0,),f(x)mx恒成立,则m的取值范围为A(,1) B(,1 C(,2) D(,2第卷二、填空题:13二项式的展开式中x2的系数是_14设x,y满足约束条件,则的最大值是_15已知sin10mcos102cos140,则m_16已知A,B是抛物线y22px(p0)上任意不同的两点,线段AB的垂直平分线与x轴相交于点P(x0,0),则x0的取值范围是_(用p表示)三、解答题:(一)必考题:17已知数列an为等差数列,a7a210,a1,a6,a21依次成等比数列(1)求数列an的通项公式;(2)设,数列bn的前n项和为Sn,若,求n的值18如图,在正方体ABCDA1B1C1D1中,点O是底面ABCD的中心,E是线段D1O的上一点(1)若E为D1O的中点,求直线OD1与平面CDE所成角的正弦值;(2)能否存在点E使得平面CDE上平面CD1O,若能,请指出点E的位置关系,并加以证明;若不能,请说明理由19随着科技的发展,网购已经逐渐融入了人们的生活在家里面不用出门就可以买到自己想要的东西,在网上付款即可,两三天就会送到自己的家门口,如果近的话当天买当天就能送到,或者第二天就能送到,所以网购是非常方便的购物方式某公司组织统计了近五年来该公司网购的人数yi(单位:人)与时间ti(单位:年)的数据,列表如下:ti12345yi2427416479(1)依据表中给出的数据,是否可用线性回归模型拟合y与t的关系,请计算相关系数r并加以说明(计算结果精确到0.01)(若|r|0.75,则线性相关程度很高,可用线性回归模型拟合)附:相关系数公式,参考数据(2)某网购专营店为吸引顾客,特推出两种促销方案方案一:每满600元可减100元;方案二:金额超过600元可抽奖三次,每次中奖的概率都为,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折两位顾客都购买了1050元的产品,求至少有一名顾客选择方案二比选择方案一更优惠的概率;如果你打算购买1000元的产品,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案20顺次连接椭圆(ab0)的四个顶点恰好构成了一个边长为且面积为的菱形(1)求椭圆C的方程;(2)A,B是椭圆C上的两个不同点,若直线OA,OB的斜率之积为(O为坐标原点),线段OA上有一点M满足,连接BM并延长椭圆C于点N,求的值21已知函数f(x)x22x2alnx,若函数f(x)在定义域上有两个极值点x1,x2,且x1x2(1)求实数a的取值范围;(2)证明:(二)选考题:22在直角坐标系xOy中,曲线(a0,t为参数)在以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,曲线(R)(1)说明C1是哪一种曲线,并将C1的方程化为极坐标方程;(2)若直线C3的方程为,设C2与C1的交点为O,M,C3与C1的交点为O,N,若OMN的面积为,求a的值23已知函数f(x)|4x1|x2|(1)解不等式f(x)8;(2)若关于x的不等式f(x)5|x2|a28a的解集不是空集,求a的取值范围高三数学考试参考答案(理科)1B 2D 3A 4C 5B 6C 7A 8B 9D10A 11C 12D 1310 145 15 16(p,)17解:(1)设数列an的公差为d,因为a7a210,所以5d10,解得d2因为a1,a6,a21依次成等比数列,所以,即(a152)2a1(a1202),解得a15所以an2n3(2)由(1)知,所以,所以,由,得n1018解:不妨设正方体的棱长为2,以DA,DC,DD1分别为x,y,z轴建立如图所示的空间直角坐标系Dxyz,则D(0,0,0),D1(0,0,2),C(0,2,0),O(1,1,0)(1)因为点E是D1O的中点,所以点E的坐标为所以,设是平面CDE的法向量,则即,取x2,则z1,所以平面CDE的一个法向量为所以所以直线OD1与平面CDE所成角的正弦值为(2)假设存在点E使得平面CDE平面CD1O,设显然,设是平面CD1O的方向量,则,即取x1,则y1,z1,所以平面CD1O的一个法向量为因为,所以点E的坐标为所以,设是平面CDE的法向量,则即取x1,则,所以平面CDE的一个法向量为因为平面CDE平面CD1O,所以,即,解得2所以的值为2即当时,平面CDE平面CD1O19解:(1)由题知,则故y与t的线性相关程度很高,可用线性回归模型拟合(2)选择方案二比方案一更优惠则需要至少中奖一次,设顾客没有中奖为事件A,则,故所求概率为若选择方案一,则需付款1000100900(元),若选择方案二,设付款X元,则X可能取值为700,800,900,1000;所以(元),因为850900,所以选择方案二更划算20解:(1)由题可知,a2b23,解得,b1所以椭圆C的方程为(2)设A(x1,y1),B(x2,y2),N(x3,y3),又,即,点N(x3,y3)在椭圆C上,即(*)A(x1,y1)
判断下列命题是否正确。 (1)若z∈C,则z2≥0; (2)若z1,z2∈C,且z1-z2>0,则z1>z2; (3)若a>b,则a+i>b+i。
正确答案: (1)错,反例:设z=i则z2=i2=-1<0;
(2)错,反例:设z1=2+i,z2=1+i,满足z1-z2=1>0,但z1、z2不能比较大小。
(3)错,因a>b,故a,b∈R,故a+i,b+i都是虚数,不能比较大小。
设随机变量X与Y相互独立,且X~N(1,2),Y~N(0,1)。令Z=-Y+2X+3,则D(Z)=()。
正确答案:9
下列数组定义语句中,不合法的是()
- A、int a[3]={0,1,2,3};
- B、int a[]={0,1,2};
- C、int a[3]={0,1};
- D、int a[3]={0};
正确答案:A
r=[w for w in range(3)],则r的值是()
- A、[0,1,2]
- B、[1,0,2]
- C、[0,1]
- D、[0,1,2,3]
正确答案:A
已知x=(0,1,2,3),那么执行语句x.add(4)之后,x的值为()
- A、{1,2,3}
- B、{1,2,3,4}
- C、{1,2}
- D、AttributeError
正确答案:D
相关考题:
- 单选题()灭火剂不可以用作扑灭易燃液体引起的火灾。A水B泡沫C一氧化碳
- 当超声波通过弹性媒质时,其声能量损失称为()A、反射B、衰减C、吸收D、散射E、折射
- 新安装或检修后的液氨储罐,应先进行()或()工作,当罐内气体氧含量小于2%或真空度不低于0.086Mpa后,方可进氨。
- 单选题空调启动瞬间电流较大,频繁开关相当(),且易损坏压缩机。A费电B费劲C麻烦D省电
- 立体主义创新的发明了()技法。A、剪切B、拼贴C、焊接D、拆分
- 单选题哪一季节最不宜发哮喘?()A春B夏C秋D冬
- 在透视下最易漏诊的是哪一种结核()A、慢性纤维空洞型肺结核B、原发综合征C、急性粟粒性肺结核D、浸润型肺结核E、结核球
- 以下哪项不是乳腺纤维腺瘤的超声表现()A、边界光滑B、有包膜C、内部呈均质低回声区D、导管扩张E、单发或多发
- 神经源性肿瘤好发部位是()A、前下纵隔B、前上纵隔C、中纵隔上部D、后纵隔脊柱旁沟内E、中纵膈下部
- 上锅厂低NOx燃烧技术有什么特点?
- 2020-2021学年山东省泰安市高二上学期期末考试化学试题 Word版-
- 2020-2021学年山东省威海市高一上学期期末考试数学试题 Word版-
- 陕西省西安市临潼区2021-2022学年高一下学期期末语文试题-
- 2020-2021学年山东省滨州市高二第一学期期末考试化学试题 Word版-
- 上海市高桥中学2021-2022学年高二下学期期中语文试题-
- 2020-2021学年山东省泰安市高一上学期期末考试语文试题 Word版-
- 浙江省湖州市2021-2022学年高一下学期期末调研测试英语试题-
- 2020-2021学年山东省德州市高一上学期期末考试物理试题 Word版-
- 江苏省南通市海安市2021-2022学年高二下学期期末数学试题-
- 安徽省阜阳市2021-2022学年高二下学期期末数学试题-