福建师范大学2021年12月《常微分方程》期末考核试题库及答案参考12

B.
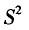
C.S
D.
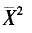


B.
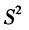
C.S
D.

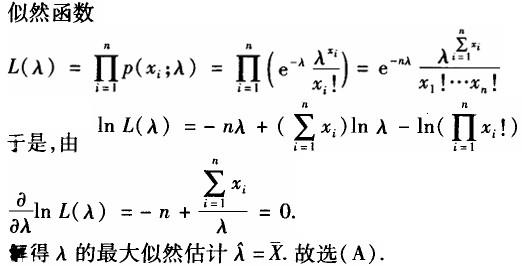
 而x1,x2,...,xn 是来自总体的样本值,则未知参数θ的最大似然估计值是:
而x1,x2,...,xn 是来自总体的样本值,则未知参数θ的最大似然估计值是:

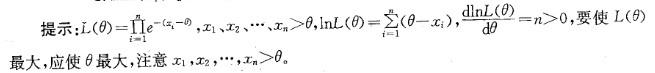
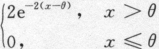 ,其中θ>0为未知参数,又设(x1,x2,…,xn)是样本(X1,X2,…,Xn)的观察值,求参数θ的最大似然估计值.
,其中θ>0为未知参数,又设(x1,x2,…,xn)是样本(X1,X2,…,Xn)的观察值,求参数θ的最大似然估计值.
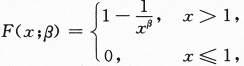
其中未知参数β>1,X1,X2,…,Xn为来自总体X的简单随机样本,求:
(Ⅰ)β的矩估计量;(Ⅱ)β的最大似然估计量.

福建师范大学2021年12月常微分方程期末考核试题库及答案参考1. 设总体X的概率密度为 其中0为待估参数从X中抽得样本X1,Xn试求的矩估计和最大似然估计设总体X的概率密度为其中0为待估参数从X中抽得样本X1,Xn试求的矩估计和最大似然估计2. ( )是函数f(x)=1/2x的原函数。A.F(x)=ln2xB.F(x)=-1/x2C.F(x)=ln(2+x)D.F(x)=lnx/2参考答案:D3. 对于函数f(x)=(x2-1)(x2-4)(2/3),下列能满足罗尔定理条件的区间是( )A.0,5B.-1,1C.-2,1D.-1,2参考答案:B4. 运输问题有可行解的充要条件是运输问题有可行解的充要条件是必要性,设xij(0)是问题的可行解,则有 从而有 充分性记,令 (i=1,2,m;j=1,2,n),则易验证(xij)满足问题,即xij)是运输问题的一个可行解 5. 设X的分布函数,求X的分布律。设X的分布函数,求X的分布律。X的概率分布律为 X -1 1 3 P 0.4 0.4 0.2 6. 火车站行李收费规定如下:当行李不超过50kg时,按每千克015元收费,当超出50kg时,超重部分按每千克火车站行李收费规定如下:当行李不超过50kg时,按每千克015元收费,当超出50kg时,超重部分按每千克025元,试建立行李收费f(x)(元)与行李重量x(kg)之间的函数关系正确答案:依题意该函数关系是其图形为平面土一折线依题意,该函数关系是其图形为平面土一折线7. 当x0时,确定无穷小量y的主要部分cxn(c是常数):y=tan(sinx)-sin(tanx)当x0时,确定无穷小量y的主要部分cxn(c是常数):y=tan(sinx)-sin(tanx)首先建立展式 事实上,将tanx表为 并利用展式2)、3)、4),得 即为所求的结果 利用此公式以及先前的展式得 由此得 8. 下列哪个函数的导数为零( )。A.cos3xB.sineC.sinxD.tan2参考答案:BD9. 以下两种陈述有何差别? (1)A1,An有一个发生; (2)A1,An恰有一个发生以下两种陈述有何差别?(1)A1,An有一个发生;(2)A1,An恰有一个发生在陈述(1),(2)中都包含了A1,An只发生一个的情况但在陈述(2)排除了A1,An中有2个或2个以上同时发生的情况,而对陈述(1)并未将这些情况排除在外,事实上我们可表述如下: A1,An有一个发生=A1An, 10. a是a与0的一个最大公因数。( )a是a与0的一个最大公因数。( )正确答案:11. 设en是内积空间X中的标准正交系,x,yX,证明设en是内积空间X中的标准正交系,x,yX,证明利用Cauchy-Schwarz即Bessel不等式可知 12. 设f(x)是连续函数,F(x)是f(x)的原函数,则( ) A当f(x)是奇函数时,F(x)必是偶函数 B当f(x)是偶函数时,F设f(x)是连续函数,F(x)是f(x)的原函数,则()A当f(x)是奇函数时,F(x)必是偶函数B当f(x)是偶函数时,F(x)必是奇函数C当f(x)是周期函数,F(x)必为周期函数D当f(x)是单调增函数,F(x)必为单调增函数13. f(x)=m|x+1|+n|x-1|,在(-,+)上( )A.连续B.仅有两个间断点x=1,它们都是可去间断点C.仅有两个间断点x=1,它们都是跳跃间断点D.以上都不对,其连续性与常数m,n有关参考答案:A14. 函数y=2008x+cosx-sinx的2008阶导数等于( )A.2008B.cosx-sinxC.sinx-cosxD.sinx+cosx参考答案:B15. 微分方程y&39;&39;-4y&39;+4y=xe2x的一个特解可设为y*=( ) Ax2e2x Bx3e2x Cx2(Ax+B)e2x De2x微分方程y-4y+4y=xe2x的一个特解可设为y*=()Ax2e2xBx3e2xCx2(Ax+B)e2xDe2xC16. 设A为n阶正交矩阵,Rn,求证设A为n阶正交矩阵,Rn,求证17. 就p,q的各种情况说明二次曲面zx2py2qz2的类型就p,q的各种情况说明二次曲面zx2py2qz2的类型正确答案:(1)pq0时zx2是抛物柱面;rn(2)q0p0时若p0zx2py2是椭圆抛物面若p0zx2py2是双曲抛物面;rn(1)pq0时,zx2,是抛物柱面;(2)q0,p0时,若p0,zx2py2是椭圆抛物面,若p0,zx2py2是双曲抛物面;18. 按分散相质点的大小不同可将分散体系分为_。按分散相质点的大小不同可将分散体系分为_。正确答案:低分子分散系;胶体分散系;粗分散系低分子分散系;胶体分散系;粗分散系19. 某环节的传遇函数为2s,则它的幅频特性的数字表达式是_,相频特性的数学表达式是_。某环节的传遇函数为2s,则它的幅频特性的数字表达式是_,相频特性的数学表达式是_。参考答案:. A()=2 () =9020. 据理回答: (1)何种函数具有“任意下和等于任意上和”的性质? (2)何种连续函数具有“所有下和(据理回答: (1)何种函数具有“任意下和等于任意上和”的性质? (2)何种连续函数具有“所有下和(或上和)都相等”的性质? (3)对于可积函数,若“所有下和(或上和)都相等”,是否仍有(2)的结论?正确答案:21. 给定三点Ai(xi,yi),i=1,2,3 求证按最小二乘拟合这三点的直线过A1A2A3的重心给定三点Ai(xi,yi),i=1,2,3 求证按最小二乘拟合这三点的直线过A1A2A3的重心记,则为A1A2A3的重心 设拟合直线为 y=a+bx, (5.7) 则a,b满足正规方程组 其中s0=3,考虑第一个方程 两边同除以3得,即点在直线(5.7)式上因而按最小二乘拟合三点Ai(i=1,2,3)的直线过A1A2A3的重心 22. 设f(x)在a,b上连续,且证明:在(a,b)内至少存在两点x1,x2,使 f(x1)=f(x2)=0设f(x)在a,b上连续,且证明:在(a,b)内至少存在两点x1,x2,使f(x1)=f(x2)=0证法1 若在a,b上f(x)0,则命题结论成立,设f(x)不恒为零,且 则F(a)=F(b)=0,又F(x)在a,b上连续,可导,可知F(x)=f(x),因此 (*) 由于F(x)为a,b上的连续函数,且,可知必定存在一点(a,b),使F()=0,否则,与(*)式矛盾, 在a,b上对F(x)利用罗尔定理,可知必定存在x1(a,),x2(,b),使得 F(x1)=f(x1)=0, F(x2)=f(x2)=0 证法2 由题设,f(x)为a,b上的连续函数,可知必定存在点x1(a,b),使f(x1)=0,否则不妨设在(a,b)内f(x)0,则与题设矛盾 设f(x)在(a,b)内不存在第二个零点,则不妨设 设g(x)=(x1-x)f(x), 则 可知 又得出矛盾,表明f(x)在(a,b)内至少存在两个零点x1,x2 23. 若f(x)=x*ex,则f&39;&39;(0)=2。( )A.错误B.正确参考答案:B24. 下面的函数哪些是一对一函数,哪些是一一对应函数: (1)f:NR,其中f(n)=log10n+1; (2)f:NR,其中 (3)f:RR下面的函数哪些是一对一函数,哪些是一一对应函数:(1)f:NR,其中f(n)=log10n+1;(2)f:NR,其中(3)f:RR,其中f(r)=2r+15(1)(2)是一对一函数,(3)是一一对应函数 本题要注意定义域和值域各自的范围 25. y+4y&39;+4y=xe-2x的特解,应设为y*=(Ax2+Bx)e-2x之形式( )y+4y+4y=xe-2x的特解,应设为y*=(Ax2+Bx)e-2x之形式()正确26. 微分方程y&39;-y=ex,满足初始条件y|x=0=1的解是( ) Ay=ex(x+1) By=xex Cy=xex+1 Dy=e-x(x+1)微分方程y-y=ex,满足初始条件y|x=0=1的解是()Ay=ex(x+1)By=xexCy=xex+1Dy=e-x(x+1)A27. 试列举所熟悉的一些代数系统试列举所熟悉的一些代数系统例如,(N,+),(Q,-),(R,),(R-0,)28. 定积分是微分的逆运算。( )A.正确B.错误参考答案:B29. 试证明: 设m(E),f(x),f1(x),f2(x),fk(x),是E上几乎处处有限的可测函数,则fk(x)在E上依测度收敛于f(试证明:设m(E),f(x),f1(x),f2(x),fk(x),是E上几乎处处有限的可测函数,则fk(x)在E上依测度收敛于f(x)的充分且必要条件是:证明 必要性 依题设知,对任给0,/2,存在N,使得 m(xE:|fk(x)-f(x)|)/2 (kN). 从而得+m(xE:|fk(x)-f(x)|)(kN)对取下确界更成立,再令k也然,由此即得所证 充分性 记Ek()=xE:|fk(x)-f(x)|,由假设知,对任给0,存在N,当kN时有从而对每个k:kN,可取k0,使得k+m(Ek(k),自然有k(kN).现在令,则(kN)因此,对任给0,0,存
 ,X1,X2,…,Xn为来自总体X的简单随机样本,求参数θ的最大似然估计量.
,X1,X2,…,Xn为来自总体X的简单随机样本,求参数θ的最大似然估计量.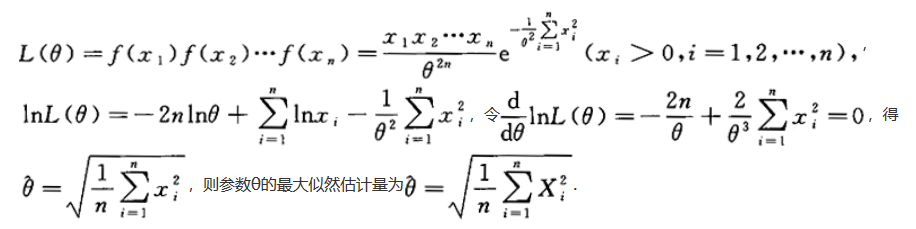

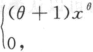 ,
,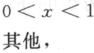 其中θ>-1是未知参数,X1,
其中θ>-1是未知参数,X1,
X2,…,Xn是来自总体X的一个容量为n的简单随机样本,分别用矩估计法和最大似然估计法求参数θ的估计量.

 ,其中未知参数θ>0,设X1,X2,…,X是来自总体X的简单样本.(1)求θ的最大似然估计量;(2)该估计量是否是无偏估计量?说明理由.
,其中未知参数θ>0,设X1,X2,…,X是来自总体X的简单样本.(1)求θ的最大似然估计量;(2)该估计量是否是无偏估计量?说明理由.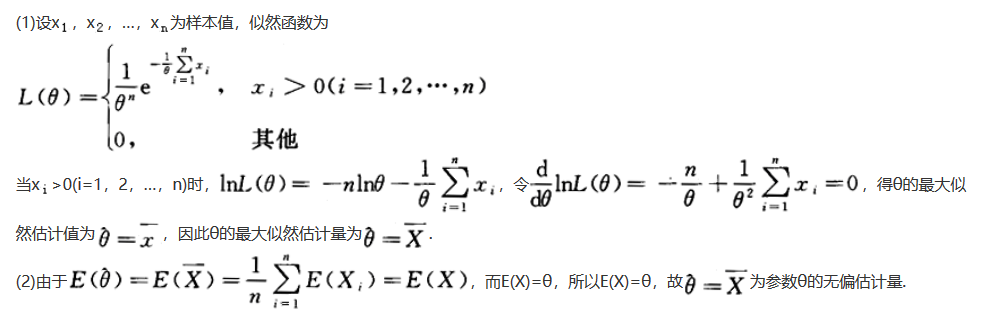
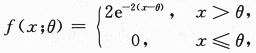
其中θ>0为未知参数.又设x1,x2,…,xn是X的一组样本观测值,求参数θ的最大似然估计值.

相关考题:
- 如何计算绝缘子配线及线槽配线工程量?
- 中国近现代创作音乐给人们留下了很多脍炙人口的音乐作品,诞生了很多优秀的创作者、革命音乐家,留给了人们极其宝贵、丰富的音乐宝藏。“龙腾国昌运,狮舞岁吉祥”,春节是中华民族最重要的传统节日。《春节序曲》是一首明快、粗犷而热烈的乐曲,由多种乐器合奏,人们之所以能分辨出不同乐器发出的声音,主要是因为它们()的不同。其作者是()A、响度;三宝B、音调;赵季平C、音色;李焕之D、节奏;聂耳
- 判断题根据天然气的组成,天然气可分为干气、湿气和酸气()。A对B错
- 指挥仪在操作使用时,除按太阳规正外,禁止测距机喵向()
- 如何计算微型电机、变频机组及电磁调速电机检查接线工程量?
- 幻想曲
- “路见不平一声吼,该出手时就出手……”电视连续剧《水游传》的主题歌《好汉歌》生动表现出梁山好汉们豪爽不羁、粗犷义气的性格。此歌的曲调取自一首民歌素材,这首民歌与下列哪个地方剧种出自同一个省()A、吕剧B、豫剧C、评剧D、黄梅戏
- CCTV《挑战主持人》2007高校系列节目给国内众多知名大学提供了展示的舞台。在内蒙古大学对决天津师范大学的一期比赛中,内蒙古大学的同学们载歌载舞,将蒙古族的艺术瑰宝呈现在了广大观众面前,获得了比赛的冠军。根据你所学的知识判断,他们表演的才艺最可能是()。A、马头琴弦子舞呼麦B、札木聂盅碗舞长调歌曲C、盅碗舞呼麦长调歌曲D、手鼓盅碗舞长调歌曲
- 民歌是人类文化中一个重要组成部分,西北民歌是指流行在山西、陕西、甘肃、宁夏、青海等省区的民歌。下列形式中流行于青海的山歌是()A、长调B、短调C、花儿D、信天游
- 判断题单量程低浓度检测仪是浓度定量检测,确定检测环境中有无燃气泄漏。A对B错