已知某篮球运动员每次投篮投中的概率为0.9.记X为他两次独立投篮投中的次数.①求X的概率分布;②求X的数学期望.
已知某篮球运动员每次投篮投中的概率为0.9.记X为他两次独立投篮投中的次数.
①求X的概率分布;
②求X的数学期望.
①求X的概率分布;
②求X的数学期望.
参考解析
解析:①设Ai=“第i次投篮投中”(i=1,2),则两次独立投篮投中的次数X的可能取值为0,1,2.
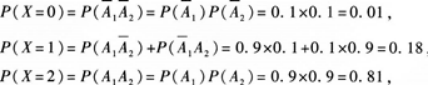
从而X的概率分布为:

②E(X)=0×0.01+1×0.18+2x0.81=1.80.
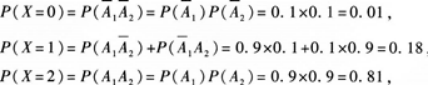
从而X的概率分布为:

②E(X)=0×0.01+1×0.18+2x0.81=1.80.
相关考题:
设随机变量X与Y相互独立,X服从参数为1的指数分布,Y的概率分布为P{Y=-1}=p,P{Y=1)=1-p,(0 (Ⅰ)求Z的概率密度; (Ⅱ)p为何值时,X与Z不相关; (Ⅲ)X与Z是否相互独立?
甲、乙两人轮流投篮。每人每次投一球。约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束。设甲每次投篮投中的概率为1/3,乙每次投篮投中的概率为1/2,且各次投篮互不影响。则投篮结束时乙只投了两个球的概率为:A.1/27B.1/9C.4/27D.13/27
李明在10场篮球比赛中的投篮情况如下(假设各场比赛互相独立): (1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率; (2)从上述比赛中选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过的0.6概率: (3)记x是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X为李明在这比赛中的命中次数,比较E(x)与x的大小(只需写出结论)。
李明在10场篮球比赛中的投篮情况如下(假设各场比赛互相独立): (1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率。 (2)从上述比赛中选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率。
问答题39.设X的概率密度为 求:(1)X的分布函数F(x); (2)P{X一0.5}.