则x=0是f(x)的:A.可去间断点 B.跳跃间断点C.振荡间断点 D.连续点
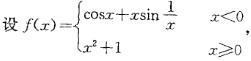则x=0是f(x)的:
A.可去间断点 B.跳跃间断点
C.振荡间断点 D.连续点
参考解析
解析：提示:求x→0+、x→0-时函数的极限值，利用可去间断点、跳跃间断点、振荡间断点、连续点定义判定，计算如下：
相关考题：
以下结论正确的是()。 A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.
以下四个命题中，正确的是（ ）A.f′（x）在（0，1）内连续，则f′（x）在（0，1）内有界B.f（x）在（0，1）内连续，则f（x）在（0，1）内有界C.f′（x）在（0，1）内连续，则f（x）在（0，1）内有界D.f（x）在（0，1）内连续，则f′（x）在（0，1）内有界
设f（x）在（-∞，+∞）二阶可导，f'（x0）=0。问f（x）还要满足以下哪个条件，则f（x0）必是f（x）的最大值？A.x=x0是f（x）的唯一驻点B.x=x0是f（x）的极大值点C.f"（x）在（-∞，+∞）恒为负值D.f"（x0）≠0
若f（-x）=f（x），且在（0，+∞）内f′（x）＞0，f″（x）＜0，则f（x）在（-∞，0）内（ ）。A.f′（x）＜0，f″（x）＜0B.f′（x）＜0，f″（x）＞0C.f′（x）＞0，f″（x）＜0D.f′（x）＞0，f″（x）＞0
下列命题正确的是（）A.函数f(x)的导数不存在的点，一定不是f(x)的极值点B.若x0为函数f(x)的驻点，则x0必为f(x)的极值点C.若函数f(x)在点x0处有极值，且f'(x0)存在，则必有f'(x0)＝0D.若函数f(x)在点x0处连续，则f'(x0)一定存在
设f（x）=|x（1-x）｜，则（ ）.《》（ ）A.x=0是f（x）的极值点，但（0，0）不是曲线y=f（x）的拐点B.x=0不是f（x）的极值点，但（0，0）是曲线y=f（x）的拐点C.x=0是f（x）的极值点，且（0，0）是曲线y=f（x）的拐点D.x=0不是f（x）的极值点，（0，0）也不是曲线y=f（x）的拐点
设f（x）的二阶导数存在，且f′（x）=f（1-x），则下列式中何式可成立（）？A、f″（x）+f′（x）=0B、f″（x）-f′（x）=0C、f″（x）+f（x）=0D、f″（x）-f（x）=0
用牛顿切线法解方程f（x）=0，选初始值x0满足（），则它的解数列{xn}n=0，1，2，…一定收敛到方程f（x）=0的根。A、f（x0）f″（x）0B、f（x0）f′（x）0C、f（x0）f″（x）0D、f（x0）f′（x）0
设f（x）在（-∞，+∞）二阶可导，f′（x0）=0。问f（x）还要满足以下哪个条件，则f（x0）必是f（x）的最大值（）？A、x=x0是f（x）的唯一驻点B、x=x0是f（x）的极大值点C、f″（x）在（-∞，+∞）恒为负值D、f″（x0）≠0
下列结论不正确的是（）。A、z=f（x，y）在点（x0，y0）处可微，则f（x，y）在点（x0，y0）处连续B、z=f（x，y）在点（x0，y0）处可微，则f（x，y）在点（x0，y0）处可导C、z=f（x，y）在点（x0，y0）处可导，则f（x，y）在点（x0，y0）处可微D、z=f（x，y）在点（x0，y0）处偏导数连续，则f（x，y）在点（x0，y0）处连续
下列结论不正确的是（）。A、y=f（x）在点x0处可微，则f（x）在点x0处连续B、y=f（x）在点x0处可微，则f（x）在点x0处可导C、y=f（x）在点x0处连续，则f（x）在点x0处可微D、y=f（x）在点x0处可导，则f（x）在点x0处连续
单选题已知函数y=f（x）对一切x满足，若f’（x0）=0（x0≠0），则（）．Af（x0）是f（x）的极大值Bf（x0）是f（x）的极小值C（x0（x0））是曲线y=f（x）的拐点Df（x0）不是f（x）的极值，（x0（x0））也不是曲线y=f（x）的拐点
单选题设函数f（x）满足关系式f″（x）＋[f′（x）]2＝x，且f′（0）＝0，则（ ）。Af（0）是f（x）的极大值Bf（0）是f（x）的极小值C点（0，f（0））是曲线y＝f（x）的拐点Df（0）不是f（x）的极值，点（0，f（0））也不是曲线y＝f（x）的拐点
单选题（2008）设函数f（x）在（-∞，+∞）上是偶函数，且在（0，+∞）内有f′（x）0，f″（x）0则在（-∞，0）内必有：（）Af′（x）0，f″（x）0Bf′（x）0，f″（x）0Cf′（x）0，f″（x）0Df′（x）0，f″（x）0
单选题设f（x）g（x）在x0处可导，且f（x0）＝g（x0）＝0，f′（x0）g′（x0）＞0，f″（x0）、g″（x0）存在，则（ ）Ax0不是f（x）g（x）的驻点Bx0是f（x）g（x）的驻点，但不是它的极值点Cx0是f（x）g（x）的驻点，且是它的极小值点Dx0是f（x）g（x）的驻点，且是它的极大值点
单选题设f（x）在（-∞，+∞）二阶可导，f（x0）=0。问f（x）还要满足以下哪个条件，则f（x0）必是f（x）的最大值？（）Ax=x0是f（x）的唯一驻点Bx=x0是f（x）的极大值点Cf″（x）在（-∞，+∞）恒为负值Df″（x）≠0
单选题设f′（x0）＝f″（x0）＝0，f‴（x0）＞0，且f（x）在x0点的某邻域内有三阶连续导数，则下列选项正确的是（ ）。Af′（x0）是f′（x）的极大值Bf（x0）是f（x）的极大值Cf（x0）是f（x）的极小值D（x0，f（x0））是曲线y＝f（x）的拐点
单选题下列说法中正确的是（ ）。[2014年真题]A若f′（x0）=0，则f（x0）必须是f（x）的极值B若f（x0）是f（x）的极值，则f（x）在点x0处可导，且f′（x0）=0C若f（x0）在点x0处可导，则f′（x0）=0是f（x）在x0取得极值的必要条件D若f（x0）在点x0处可导，则f′（x0）=0是f（x）在x0取得极值的充分条件
单选题设f（x）在x＝0处满足f′（0）＝f″（0）＝…＝f（n）（0），f（n＋1）（0）＞0，则（ ）。A当n为偶数时，x＝0是f（x）的极大值点B当n为偶数时，x＝0是f（x）的极小值点C当n为奇数时，x＝0是f（x）的极大值点D当n为奇数时，x＝0是f（x）的极小值点
单选题若f（－x）＝－f（x）（－∞＜x＜＋∞），且在（－∞，0）内f′（x）＞0，f″（x）＜0，则f（x）在（0，＋∞）内是（ ）。[2013年真题]Af′（x）＞0，f″（x）＜0Bf′（x）＜0，f″（x）＞0Cf′（x）＞0，f″（x）＞0Df′（x）＜0，f″（x）＜0
单选题设f（x）在（-∞，+∞）二阶可导，f′（x0）=0。问f（x）还要满足以下哪个条件，则f（x0）必是f（x）的最大值（）？Ax=x0是f（x）的唯一驻点Bx=x0是f（x）的极大值点Cf″（x）在（-∞，+∞）恒为负值Df″（x0）≠0
单选题设f（x）的二阶导数存在，且f′（x）=f（1-x），则下列式中何式可成立（）？Af″（x）+f′（x）=0Bf″（x）-f′（x）=0Cf″（x）+f（x）=0Df″（x）-f（x）=0
单选题（2013）若f（-x）=-f（x）（-∞0，f″（x）0，则f（x）在（0，+∞）内是：（）Af′（x）0，f″（x）0Bf′（x）0，f″（x）0Cf′（x）0，f″（x）0Df′（x）0，f″（x）0
单选题设f（x）在（－∞，＋∞）可导，x0≠0，（x0，f（x0））是y＝f（x）的拐点，则（ ）。Ax0必是f′（x）的驻点B（－x0，－f（x0））必是y＝－f（－x）的拐点C（－x0，－f（x0））必是y＝－f（x）的拐点D对∀x＞x0与x＜x0，y＝f（x）的凸凹性相反