下列说法正确的是( )。A.对回归方程显著性检验,一般采用的方法是方差分析法B.根据F>Fa(1,n-2),可以得出销售量y和气温x的线性相关关系是高度显著的结论C.当n很大且x0十分接近于x时,y0的预测区间可近似地表示为:D.小样本条件下,对于给定的x0=35,α=0.01,tα/2=1.86,饮料销售量y0预测区间为:(328,588)
下列说法正确的是( )。
A.对回归方程显著性检验,一般采用的方法是方差分析法
B.根据F>Fa(1,n-2),可以得出销售量y和气温x的线性相关关系是高度显著的结论
C.当n很大且x0十分接近于x时,y0的预测区间可近似地表示为: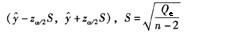
D.小样本条件下,对于给定的x0=35,α=0.01,tα/2=1.86,饮料销售量y0预测区间为:(328,588)
相关考题:
下列方法不可以用来检验回归方程显著性的是( )。A.相关系数法。对于给定的显著性水平α,当相关系数r的绝对值大于临界值r1-α/2(n-2)时,便认为两个变量间存性关系,所求得的回归方程是显著性的B.方差分析法C.计算F比,对于给定的显著性水平α,当F>F1-α(fR,fE)时,认为回归方程显著D.定性分析法
关于变量销售量y和气温x的相关系数和检验的说法正确的是( )。A.相关系数为0.8518B.需要查相关系数显著性检验表,α一定时,自由度为8的r值C.若α=0.01,相关系数大于相关系数显著性检验值,则可判断出销售量y和气温x之间的线性相关关系对于α=0.01是显著的D.若α=0.01,相关系数大于相关系数显著性检验值,则可判断出销售量y和气温x之间的线性相关关系对于α=0.01是不显著的
下列说法正确的是A.若|r|>r0.01(n-2),变量X,Y间一定有直线关系B.若|r|>r0.01(n-2),则变量X,Y间有正相关关系C.若X,Y间有相关关系,则说明X, Y间一定有因果关系D.用最小二乘法确定直线回归方程的原则是各观察点与直线的垂直距离的平方和最小E.回归系数的假设检验可以用t检验和 F检验,也可以用r的检验代替
下列关于回归方程的显著性检验的说法正确的有( )。A.检验两个变量间是否存性相关关系的问题便是对回归方程的显著性检验问题B.建立回归方程的目的是表达两个具有线性相关的变量间的定量关系,因此只有当两个变量间具有线性关系,即回归是显著的,这时建立的回归方程才是有意义的C.求两个变量间相关系数,对于给定的显著水平,仅当相关系数r的绝对值大于临界值r1-α/2(n-2)时,便认为两个变量间存性相关关系,所求得的回归是显著的,即回归方程是有意义的D.为了推广到多元线性回归场合,另一种检验方法是方差分析的方法嚣.当SR,SE,fA,fE已知,对于给定的显著性水平α,当F<f1-α(fA,fE)时,认为回归方程显著,即是有意义的
函数z=f(x,y)处可微分,且fx'(x0,y0)=0,fy'(x0,:y0)=0,则f (x,y)在P0(x0,y0)处有什么极值情况?A.必有极大值B.必有极小值C.可能取得极值D.必无极值
函数z=f(x,y)在P0 (x0,y0)处可微分,且f'x (x0,y0)=0,f'y(x0,y0)=0,则f(x,y)在P0 (x0,y0)处有什么极值情况?A.必有极大值 B.必有极小值C.可能取得极值 D.必无极值
两个变量(X,Y),其观测值(xi,yi), i =1, 2,…n,若显著性水平为a,相关系数为r,则下列说法正确的有( )。A. -1≤r≤1B. r=0,x, y间存在线性相关C. r= -1,完全负线性相关D.相关系数检验的临界值表示为r1-a/2(n-2)E. r=0, x,y可能存在某种函数关系
下列关于回归方程的显著性检验的说法正确的有( )。A.检验两个变量间是否存在线性相关关系的问题便是对回归方程的显著性检验问题B.建立回归方程的目的是表达两个具有线性相关的变量间的定量关系,因此只有当两个变量间具有线性关系,即回归是显著的,这时建立的回归方程才是有意义的C.求两个变量间相关系数,对于给定的显著水平,仅当相关系数r的绝对值大于临界值r1-a/2(n-2)时,便认为两个变量间存在线性相关关系,所求得的回归是显著的,即回归方程是有意义的D.为了推广到多元线性回归场合,另一种检验方法是方差分析的方法E.当SR,SE,fA,fE已知,对于给定的显著性水平a,F1-a(fA,fE)时,认为回归方程显著,即是有意义的
根据某地区 1966-2015 年的亩产量(公斤,y)/降雨量(毫米、 )以及气温(度,)的统计数据进行回归分析,得如下结果:y?? -834.05? 2.6869x?+59.0323x?R=0.9193, R2=0.8451 调整 R2=0.8269请根据上述资料回答下列问题:对于回归方程来说,( )A.t 检验是检验解释变量Xi对因变量 y 的影响是否显著B.t 检验是从回归效果检验回归方程的显著性C.F 检验是检验解释变量Xi对因变量 y 的影响是否显著D.F 检验是从回归效果检验回归方程的显著性
下列关于t检验与F检验的说法正确的有( )。Ⅰ.对回归方程线性关系的检验是F检验Ⅱ.对回归方程线性关系的检验是t检验Ⅲ.对回归方程系数显著性进行的检验是F检验Ⅳ.对回归方程系数显著性进行的检验是t检验A.Ⅰ.Ⅱ.ⅢB.Ⅰ.ⅣC.Ⅰ.Ⅲ.ⅣD.Ⅰ.Ⅱ.Ⅳ
下列结论不正确的是()。A、z=f(x,y)在点(x0,y0)处可微,则f(x,y)在点(x0,y0)处连续B、z=f(x,y)在点(x0,y0)处可微,则f(x,y)在点(x0,y0)处可导C、z=f(x,y)在点(x0,y0)处可导,则f(x,y)在点(x0,y0)处可微D、z=f(x,y)在点(x0,y0)处偏导数连续,则f(x,y)在点(x0,y0)处连续
由于回归方程是由数理统计得出的,它反映的是实际数据的统计规律,所以,根据回归方程所得的预测值y0只是对应于x0的单点预测估计值,预测值应该有一个()A、相关系数B、自由度C、显著性水平D、置信区间
单选题以下关于二元函数的连续性的说法正确是( )。A若f(x,y)沿任意直线y=kx在点x=0处连续,则f(x,y)在(0,0)点连续B若f(x,y)在点(x0,y0)点连续,则f(x0,y)在y0点连续,f(x,y0)在x0点连续C若f(x,y)在点(x0,y0)点处偏导数fx′(x0,y0)及fy′(x0,y0)存在,则f(x,y)在(x0,y0)处连续D以上说法都不对
多选题关于回归方程的显著性检验的说法正确的是()A检验两个变量间是否存在线性相关关系的问题便是对回归方程的显著性检验问题B建立回归方程的目的是表达两个具有线性相关的变量间的定量关系,因此只有当两个变量间具有线性关系,即回归是显著的,这时建立的回归方程才是有意义的C求两个变量间相关系数,对于给定的显著水平α,当相关系数r的绝对值大于临界值r1-α/2(n-2)时,便认为两个变量间存在线性相关关系,所求得的回归是显著的,即回归方程是有意义的D为了推广到多元线性回归场合,另一种检验方法是方差分析的方法
单选题由于回归方程是由数理统计得出的,它反映的是实际数据的统计规律,所以,根据回归方程所得的预测值y0只是对应于x0的单点预测估计值,预测值应该有一个()A相关系数B自由度C显著性水平D置信区间
单选题设f(x,y)与φ(x,y)均为可微函数,且φy′(x,y)≠0。已知(x0,y0)是f(x,y)在约束条件φ(x,y)=0下的一个极值点,下列选项正确的是( )。A若fx′(x0,y0)=0,则fy′(x0,y0)=0B若fx′(x0,y0)=0,则fy′(x0,y0)≠0C若fx′(x0,y0)≠0,则fy′(x0,y0)=0D若fx′(x0,y0)≠0,则fy′(x0,y0)≠0
多选题两个变量(x,y),其观测值为(xi,yi),i=1,2,…,若显著性水平为α,相关系数为r,则下列说法正确的有( )。A-1≤r≤1Br=0,x、y间存在线性相关Cr=-1,完全负线性相关D相关系数检验的临界值表示为r1-α/2(n-2)Er=0,x、y可能存在某种函数关系
多选题下列关于回归方程的显著性检验的说法正确的有( )。A检验两个变量间是否存在线性相关关系的问题便是对回归方程的显著性检验问题B建立回归方程的目的是表达两个具有线性相关的变量间的定量关系,因此只有当两个变量间具有线性关系,即回归是显著的,这时建立的回归方程才是有意义的C求两个变量间相关系数,对于给定的显著水平,仅当相关系数r的绝对值大于临界值r1-α/2(n-2)时,便认为两个变量间存在线性相关关系,所求得的回归是显著的,即回归方程是有意义的D为了推广到多元线性回归场合,另一种检验方法是方差分析的方法E当SR,SE,fA,fE已知,对于给定的显著性水平α,当F<F1-α(fA,fE)时,认为回归方程显著,即是有意义的
单选题可微函数f(x,y)在点(x0,y0)取得极小值,下列结论正确的是( )。Af(x0,y)在y=y0处的导数等于零Bf(x0,y)在y=y0处的导数大于零Cf(x0,y)在y=y0处的导数小于零Df(x0,y)在y=y0处的导数不存在
单选题下列方法不可以用来检验回归方程显著性的是( )。A相关系数法。对于给定的显著性水平α,当相关系数r的绝对值大于临界值r1-α/2(n-2)时,便认为两个变量间存在线性关系,所求得的回归方程是显著性的B方差分析法C计算F比,对于给定的显著性水平α,当F>F1-α(fR,fE)时,认为回归方程显著D定性分析法