设函数f(x)在(-∞，+∞)内单调有界，{xn}为数列，下列命题正确的是A.若{xn}收敛，则{f(xn)}收敛B.若{xn}单调，则{f(nx)}收敛C.若{f(xn)}收敛，则{xn}收敛D.若{f(xn)}单调，则{xn}收敛
设函数f(x)在(-∞，+∞)内单调有界，{xn}为数列，下列命题正确的是
A.若{xn}收敛，则{f(xn)}收敛
B.若{xn}单调，则{f(nx)}收敛
C.若{f(xn)}收敛，则{xn}收敛
D.若{f(xn)}单调，则{xn}收敛
B.若{xn}单调，则{f(nx)}收敛
C.若{f(xn)}收敛，则{xn}收敛
D.若{f(xn)}单调，则{xn}收敛
参考解析
解析：(方法一)由于{xn}单调，f(xn)单调有界，则数列{f(xn)}单调有界.由单调有界准则知数列{f(xn)}收敛，故应选(B). (方法二)排除法：若取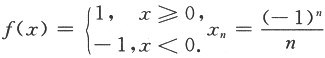
，则显然f(xn)单调，{xn}收敛，但显然{f(xn)}不收敛，这样就排除了(A).若取f(xn)=arctanx，x=n，则f(xn)=arctann，显然{f(xn)}收敛且单调，但{xn}不收敛，这样就排除了(C)和(D)，故应选(B).
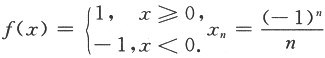，则显然f(xn)单调，{xn}收敛，但显然{f(xn)}不收敛，这样就排除了(A).若取f(xn)=arctanx，x=n，则f(xn)=arctann，显然{f(xn)}收敛且单调，但{xn}不收敛，这样就排除了(C)和(D)，故应选(B).
相关考题：
下列命题中，哪个是正确的？A.周期函数f（x）的傅立叶级数收敛于f（x）B.若f（x）有任意阶导数，则f（x）的泰勒级数收敛于f（x）C.若正项级数收敛，则必收敛D.正项级数收敛的充分且必-条件是级数的部分和数列有界
以下四个命题中，正确的是（ ）A.f′（x）在（0，1）内连续，则f′（x）在（0，1）内有界B.f（x）在（0，1）内连续，则f（x）在（0，1）内有界C.f′（x）在（0，1）内连续，则f（x）在（0，1）内有界D.f（x）在（0，1）内连续，则f′（x）在（0，1）内有界
根据f(x)的导函数f'(x)的图像，判定下列结论正确的是（）A.在(－∞，－1)内，f(x)是单调增加的B.在(－∞，0)内，f(x)是单调增加的C.f(－1)为极大值D.f(－1)为极小值
下列命题中，正确的是( ).A.单调函数的导函数必定为单调函数B.设f(x)为单调函数，则f(x)也为单调函数C.设f(x)在(a，b)内只有一个驻点xo，则此xo必为f(x)的极值点D.设f(x)在(a，b)内可导且只有一个极值点xo，f(xo)=0
设?(x)为开区间(a，b)上的可导函数，则下列命题正确的是（ ）A.(x)在(a，b)上必有最大值B.(x)在(a，b)上必一致连续C.(x)在(a，b)上必有界D.(x)在(a，b)上必连续
单选题设f（x）在（－∞，＋∞）内可导，且对任意x2＞x1，都有f（x2）＞f（x1），则正确的结论是（ ）。A对任意x，f′（x）＞0B对任意x，f′（x）≤0C函数－f（－x）单调增加D函数f（－x）单调增加
单选题设函数f（x）在区间[1，＋∞）内二阶可导，且满足条件f（1）＝f′（1）＝0，x＞1时f″（x）＜0，则g（x）＝f（x）/x在（1，＋∞）内（ ）。A曲线是向上凹的B曲线是向上凸的C单调减少D单调增加
单选题设函数f（x）在（－∞，＋∞）内单调有界，{xn}为数列，下列命题正确的是（ ）。A若{xn}收敛，则{f（xn）}收敛B若{xn}单调，则{f（xn）}收敛C若{f（xn）}收敛，则{xn}收敛D若{f（xn）}单调，则{xn}收敛