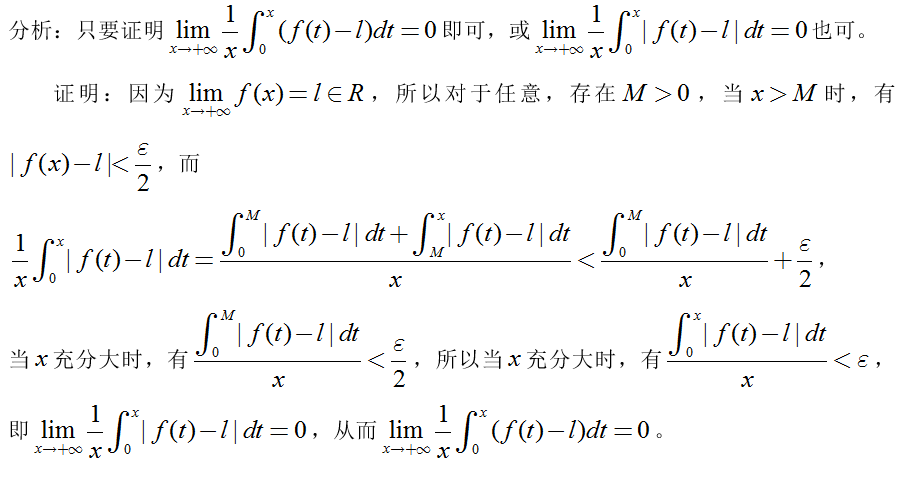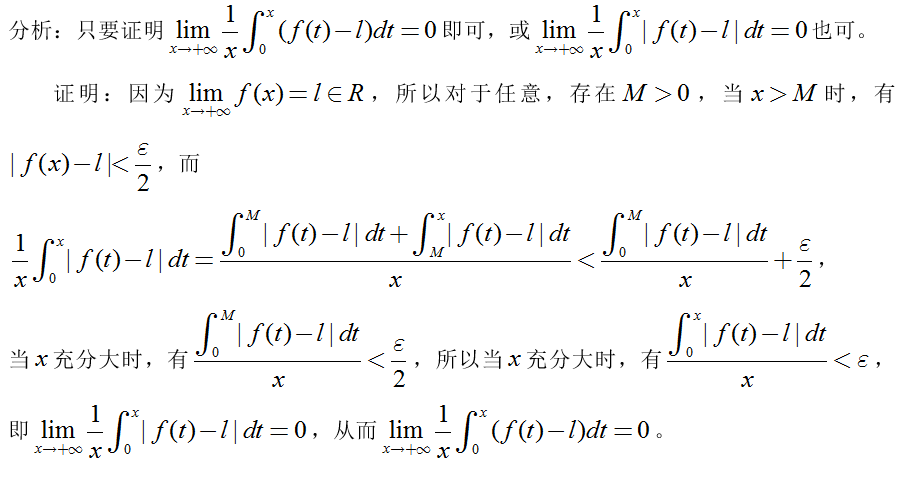连续型随机变量,其取值为________。A.仅取数轴上有限个点B.取数轴上无限可列个点C.取数轴上的任意点D.取数轴上某一区间上所有的点
关于可导性,下列说法正确的是()。 A、在区间上都是可导的B、在区间上都不可导C、在区间上除外都是可导的D、以上说法都不对
设函数在开区间上连续,则函数在该区间上一定有最大最小值。() 此题为判断题(对,错)。
区间[a,b]上的三次样条插值函数是() A、在[a,b]上2阶可导,节点的函数值已知,子区间上为3次多项式B、在区间[a,b]上连续的函数C、在区间[a,b]上每点可微的函数D、在每个子区间上可微的多项式
设一有限时间区间上的连续时间信号,其频谱分布的区间是()。 A、有限B、无穷C、连续区间D、离散区间
设函数f(x)在区间[a,b]上连续,则下列结论中哪个不正确?D.f(x)在[a,b]上是可积的
函数f(x)在区间[a,b]上连续是它在该区间上可积的( ).A.充分条件B.必要条件C.充要条件D.无关条件
设f(x)在闭区间[0,1]上连续,在(0,1)内可导,且f(0)=0,
设X1,X2,…,X100相互独立且在区间[-1,1]上同服从均匀分布,则由中心极限定理≈_______.
设A、B、C为同阶矩阵,且C为非奇异矩阵,满足,求证:
设函数f(x)在区间[0,1]上具有2阶导数,且,证明: (Ⅰ)方程f(x)=0在区间(0,1)内至少存在一个实根; (Ⅱ)方程在区间(0,1)内至少存在两个不同实根.
盈余公积金包括______和_____。()A:法定盈余公积;任意盈余公积B:资本公积;任意盈余公积C:任意盈余公积;决议盈余公积D:自由盈余公积;有限盈余公积
设f(x)在[a,b]上可导,且f(a)f(b)小于0,
函数f(x)在[a,b]上黎曼可积的必要条件是f(x)在[a,b]上( )。A.可微B.连续C.不连续点个数有限D.有界
罗尔定理:设函数(x)满足条件:(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;(3)(a)=(b),则在(a,b)内至少存在一点ξ,使得,′(ξ)=0。证明这个定理并说明其几何意义。
设随机变量X,Y相互独立,且X~N(μ,σ2),Y在[a,b]区间上服从均匀分布,则D(X-2Y)=()。
设 (x)在[a,b]上连续,在(a,b)内可导,且 (a)= (b),则( )。
关于原点对称的区间上可积的奇函数的定积分一定为零。
设:一有限时间区间上的连续时间信号,其频谱分布的区间是()。A、有限,连续区间B、无穷,连续区间C、有限,离散区间D、无穷,离散区间
盈余公积金主要包括()。A、法定盈余公积和任意盈余公积B、资本公积和任意盈余公积C、任意盈余公积和决议盈余公积D、自由盈余公积和有限盈余公积
盈余公积金包括_________和_________。( )A、法定盈余公积;任意盈余公积B、任意盈余公积;决议盈余公积C、自由盈余公积;有限盈余公积
问答题设函数f(x)在闭区间[0,1]上可微,对于[0,1]上的每一个x,函数f(x)的值都在开区间(0,1)内,且f′(x)≠1,证明在(0,1)内有且仅有一个x,使得f(x)=x。
问答题设不恒为常数的函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b)。证明:在(a,b)内至少存在一点ξ,使得f′(ξ)>0。
问答题设f(x)在[a,b]上连续,在(a,b)内可导,且f(a)·f(b)>0,f(a)·f[(a+b)/2]<0。试证:对任意实数k,∃ξ∈(a,b),使得f′(ξ)=kf(ξ)。
单选题盈余公积金包括_________和_________。( )A法定盈余公积;任意盈余公积B任意盈余公积;决议盈余公积C自由盈余公积;有限盈余公积
单选题盈余公积金主要包括()。A法定盈余公积和任意盈余公积B资本公积和任意盈余公积C任意盈余公积和决议盈余公积D自由盈余公积和有限盈余公积
单选题设P(x)是在区间[α,b]上的y=f(x)川的分段线性插值函数,以下条件中不是P(x)必须满足的条件为( )。AP(x)在[a,b]上连续BP(Xk)=YkCP(x)在[α,b]上可导DP(x)在各子区间上是线性函数
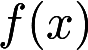 在任意有限区间上可积且
在任意有限区间上可积且 ,求证
,求证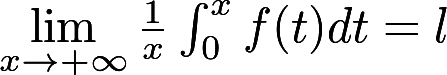 。
。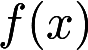 在任意有限区间上可积且
在任意有限区间上可积且 ,求证
,求证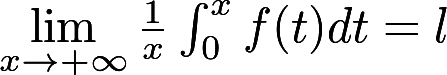 。
。