下列关于两个相互独立的随机变量X1和X2的标准差和方差表达式,正确的是( )。
下列关于两个相互独立的随机变量X1和X2的标准差和方差表达式,正确的是( )。
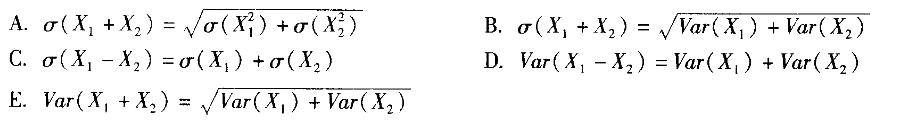
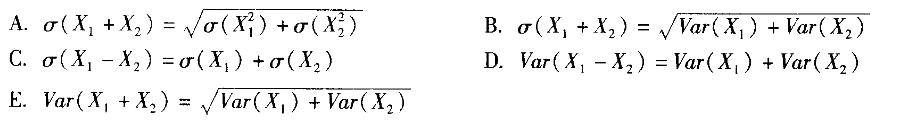
参考解析
解析:X1和X2相互独立时,有: 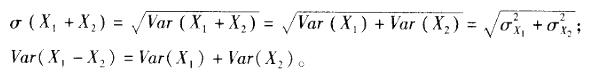
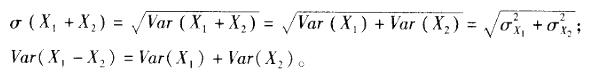
相关考题:
关于随机变量特征数的表达式不正确的是( )。A.E(aX+b)=aE(X)+bB.F(X1+X2)=E(X1)+E(X2)C.var(X1±X2)=var(X1)+var(X2)D.var(aX+b)=avar(X)
下列关于随机变量特征数的描述有误的是( )。A.均值用来表示分布的中心位置用E(X)表示B.方差用来表示分布的散布大小,用Var(X)表示C.标准差是方差的平方,实际中更常用标准差来表示分布的散布的大小D.离均值越近的值发生的可能性越大E.对于独立的随机变量,其方差和标准差具有可加性
设随机变量X1,X2,…,Xn相互独立,Sn=X1+X2+…+Xn,则根据列维一林德伯格中心极限定理,当n充分大时,Sn近似服从正态分布,只要X1,X2,…,Xn( )。A.有相同的数学期望B.有相同的方差C.服从同一指数分布D.服从同一离散型分布
下列关于两个相互独立的随机变量X1和X2的标准差和方差表达式,正确的是( )。A.σ(X1+X2)=B.σ(X1+X2)=C.σ(X1-X2)=σ(X1)+σ(X2)D.Var(X1-X2)=Var(X1)+Var(X2)E.Var(X1+X2)=
设X1,X2,…,Xn,…相互独立,则X1,X2,…,Xn,…满足辛钦大数定律的条件是( ) A.X1,X2,…,Xn,…同分布且有相同的数学期望与方差B.X1,X2,…,Xn,…同分布且有相同的数学期望C.X1,X2,…,Xn,…为同分布的离散型随机变量D.X1,X2,…,Xn,…为同分布的连续型随机变量
设随机变量X1,X2,…,Xn相互独立,Sn=X1,X2,…,Xn则根据列维林德伯格(Levy-Lindberg)中心极限定理,当n充分大时,Sn近似服从正态分布,只要1,X2,…,XnA.有相同的数学期望.B.有相同的方差.C.服从同一指数分布.D.服从同一离散分布.
设随机变量X1和X2相互独立,它们的均值分别为3与4,方差分别为1与2,则 Y = 4X1+2X2的均值与方差分别为( )。A. E (Y) =4 B. E (Y) =20C.Var (Y) =14 D.Var (Y) =24E.Var (Y) =15
已知样本x1,x2,…,xn,其中μ未知。下列表达式中,不是统计量的是()。A. X1 +X2 B. max(x1,x2,…,xn)C. X1 +X2 -2μ D. (X1 -μ)/σE. X1 +μ
相关系数是反映两个随机变量之间线性相关程度的统计指标,如果两个随机变量X和Y之间协方差为0.0031,方差分别为0.04和0.09,据此可以判断X和Y之间是( )。 A、极弱相关B、相互独立C、中度相关D、高度相关
关于中心极限定理的描述正确的是:()。A、对于n个相互独立同分布的随机变量共同服从正态分布,则样本均值又仍为正态分布B、正态样本均值服从分布N(μ,σ2/n)C、设X1,X2,„,Xn为n个相互独立共同分布随机变量,其共同分布不为正态分布或未知,但其均值和方差都存在,则在n相当大时,样本均值近似服从正态分布D、无论共同分布是什么,只要变量个数n相当大时,均值的分布总近似于正态分布
多选题下列关于随机变量特征数的描述有误的有( )。A均值用来表示分布的中心位置用E(X)表示B方差用来表示分布的散布大小,用Var(X)表示C标准差是方差的平方,实际中更常用标准差来表示分布的散布的大小D离均值越近的值发生的可能性越大E对于独立的随机变量,其方差和标准差具有可加性
多选题关于中心极限定理的描述正确的是:()。A对于n个相互独立同分布的随机变量共同服从正态分布,则样本均值又仍为正态分布B正态样本均值服从分布N(μ,σ2/n)C设X1,X2,„,Xn为n个相互独立共同分布随机变量,其共同分布不为正态分布或未知,但其均值和方差都存在,则在n相当大时,样本均值近似服从正态分布D无论共同分布是什么,只要变量个数n相当大时,均值的分布总近似于正态分布
多选题设随机变量X1与X2相互独立,它们的均值分别为3与4,方差分别为1与2,则Y=4X1-2X2的均值与方差分别为( )。AE(Y)=4BE(Y)=20CVar(Y)=8DVar(Y)=14EVar(Y)=24
填空题设随机变量X1,X2,X3相互独立,其中X1在[0,6]上服从均匀分布,X2~N(0,22),X3服从参数为λ=3的泊松分布,记随机变量Y=X1-2X2+3X3,则D(Y)=____。
多选题设随机变量X1与X2相互独立,它们的均值分别为3与4,方差分别为1与2,则y=4X1αX2的均值与方差分别为( )。AE(y)=4BE(y)=20CVar(y)=14DVar(y)=24EVar(y)=15