设X~N(μ, σ2),当分布中心与产品规范中心重合时,下列结论成立的有( )。A. X落在(μ-σ,μ+σ)内的概率为68. 27 %B. X落在(μ-2σ,μ+2σ)内的概率为95.45%C. X落在(μ-3σ,μ+3σ)内的概率为99.73%D. X落在(μ-4σ,μ+4σ)外的概率为0.002PPmE. X落在(μ-6σ,μ+6σ)外的概率为0.002ppm
设X~N(μ, σ2),当分布中心与产品规范中心重合时,下列结论成立的有( )。
A. X落在(μ-σ,μ+σ)内的概率为68. 27 %
B. X落在(μ-2σ,μ+2σ)内的概率为95.45%
C. X落在(μ-3σ,μ+3σ)内的概率为99.73%
D. X落在(μ-4σ,μ+4σ)外的概率为0.002PPm
E. X落在(μ-6σ,μ+6σ)外的概率为0.002ppm
A. X落在(μ-σ,μ+σ)内的概率为68. 27 %
B. X落在(μ-2σ,μ+2σ)内的概率为95.45%
C. X落在(μ-3σ,μ+3σ)内的概率为99.73%
D. X落在(μ-4σ,μ+4σ)外的概率为0.002PPm
E. X落在(μ-6σ,μ+6σ)外的概率为0.002ppm
参考解析
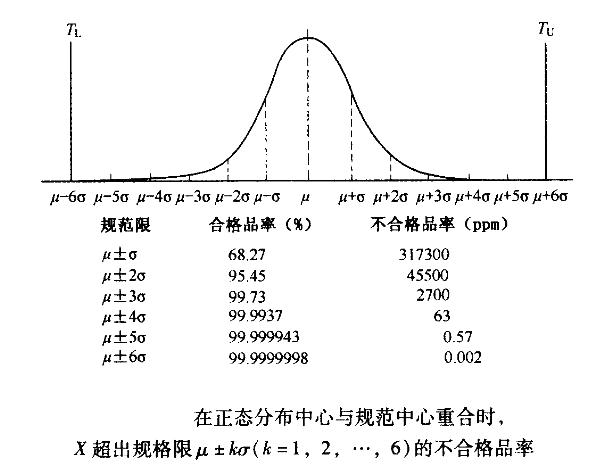
解析:在正态分布X~N(μ, σ2)中,正态分布的中心μ与规范中心M=(TU+ TL)/2重合时,若规范限取为μ±kσ,其中k为某个实数,则有:①合格品率=P( X-μ ≤kσ)=20(Φ) -1;②不合格品率=P(( X-μ >kσ) =2[1 - Φ(k)];对k=1,2,3,4,5,6,具体计算结果如图所示,其中不合格品率用ppm(10-6)单位表示。

相关考题:
设X~N(μ,σ2),当分布中心与产品规范中心重合时,下列结论成立的有( )。A.X落在(μ-σ,μ+σ)内的概率为68.27%B.X落在(μ-2σ,σ+2σ)内的概率为95.45cC.X落在(μ-3σ,μ+3σ)内的概率为99.73%D.X落在(μ-4σ,μ+4σ)外的概率为0.002ppmE.X落在(μ-6σ,μ+6σ)外的概率为0.002ppm
当产品质量特性值分布的均值与公差中心重合时,( )。 A.过程能力指数增大,不合格品率减小 当产品质量特性值分布的均值与公差中心重合时,( )。A.过程能力指数增大,不合格品率减小B.过程能力指数增大,不合格品率增大C.过程能力指数减小,不合格品率增大D.不合格品率不变,过程能力指数减小
t分布与标准正态分布之间存在的关系是A.曲线下中间95%面积对应的分位点均为±1.96B.当u增大时,二曲线的中心位置右移C.当n为∞时,t分布与正态分布一致D.当n为∞时,t分布与标准正态分布一致E.两者均为以0为中心,a为l的钟形分布
设随机变量X1,X2,…,Xn相互独立,Sn=X1+X2+…+Xn,则根据列维一林德伯格中心极限定理,当n充分大时,Sn近似服从正态分布,只要X1,X2,…,Xn( )。A.有相同的数学期望B.有相同的方差C.服从同一指数分布D.服从同一离散型分布
t分布与标准正态分布之间存在的关系是A、曲线下中间95%面积对应的分位点均为±1.96B、当μ增大时,二曲线的中心位置右移C、当n为∞时,t分布与正态分布一致D、当n为∞时,t分布与标准正态分布一致E、两者均为以0为中心,σ为1的钟形分布
正态分布计算所依据的重要性质为( )。A.设X~N(μ,σ2),则u=(X-μ)/σ~N(0,1)B.设X~N(μ,σ2),则对任意实数a、b有P(X<b)=Ф[(b-μ)/σ)C.设X~N(μ,σ2),则对任意实数a、b有P(X>a)=1-Ф[(a-μ)/σ]D.设X~N(μ,σ2),则对任意实数a、b有P(a<X<b)=Ф[(b-μ)/σ)-Ф[(a-μ)/σ]E.设X~μ(μ1,,Y~N(μ2,,则X+Y~N(μ1+μ2,(σ1+σ2) 2)
设某产品长度X~N(15,0.05 2,)若产品长度的规范限为l5±0.1,则不合格品率为( )。A.Ф(2)+ Ф(-2)S 设某产品长度X~N(15,0.05 2,)若产品长度的规范限为l5±0.1,则不合格品率为( )。A.Ф(2)+ Ф(-2)B.2Ф(-2)C.2Ф(2)D.2[1-Ф(2)]E.Ф(2)-Ф(-2)
设Xi(i=1,2,…,n)为n个相互独立的随机变量,则下列结论成立的是( )。A.若Xi(i=1,2,…,n)服从正态分布,且分布参数相同,则服从正态分布B.若Xi(i=1,2,…,n)服从指数分布,且λ相同,则服从正态分布C.若Xi(i=1,2,…,n)服从[a,b]上的均匀分布,则服从正态分布D.无论Xi(i=1,2,…,n)服从何种相同的分布,其均值都服从正态分布
设Xi (i=1,2,…,n)为n个相互独立的随机变量,则下列结论成立的是( )。A.若Xi (i=1,2,…,n)服从正态分布,且分布参数相同,则服从正态分布B.若Xi (i=1,2,…,n)服从指数分布,且λ相同,则服从正态分布C.若Xi(i=1,2,…,n)服从[a,b)上的均匀分布,则服从正态分布D.无论Xi (i=1,2,…,n)服从何种分布,其均值都服从正态分布
设随机变量X1,X2,…,Xn相互独立,Sn=X1,X2,…,Xn则根据列维林德伯格(Levy-Lindberg)中心极限定理,当n充分大时,Sn近似服从正态分布,只要1,X2,…,XnA.有相同的数学期望.B.有相同的方差.C.服从同一指数分布.D.服从同一离散分布.
设X~N(0,1),则下列各式成立的有( )。A. P(X>a)=P(X≥a) =1 -Φ(a) B. P(a≤X≤b) =Φ(b) -Φ(a)C. P( X ≤a) =2Φ(a) -1 D. Φ(-a) = -Φ(a)E. P(X
正态分布计算所依据的重要性质为( )。A.设X~N(μ,σ2),则μ= (X-μ)/σ~N(0, 1)B.设X~N(μ,σ2),则对任意实数a、b有P(XC.设X~N(μ,σ2),则对任意实数a、b有P(X>a) =1-Φ[(a-μ)/σ]D.设X~N(μ,σ2),则对任意实数a、b有P(a
连续变量x服从正态分布N(μ,σ2),当变动σ,而μ不变时,正态分布的曲线会()A、改变中心,也改变曲线的形状B、不改变中心,改变曲线的形状C、改变中心,不改变曲线的形状D、不改变中心,也不改变曲线的形状
设(X1,X2,…,X)是抽自正态总体N(0,1)的一个容量为n的样本,记,则下列结论中正确的是()。A、服从正态分布N(0,1)B、n服从正态分布N(0,1)C、服从自由度为n的x2分布D、服从自由度为(n-1)的t分布
多选题设X~N(0,1),则下列各式成立的有( )。AP(X>a)=P(X≥a)=1-Φ(a)BP(a≤X≤b)=Φ(b)-Φ(a)CP(|X|≤a)=2Φ(a)-1DΦ(-a)=-Φ(a)EP(X<a)=P(X≥a)=1-Φ(a)
单选题设(X1,X2,…,X)是抽自正态总体N(0,1)的一个容量为n的样本,记,则下列结论中正确的是()。A服从正态分布N(0,1)Bn服从正态分布N(0,1)C服从自由度为n的x2分布D服从自由度为(n-1)的t分布
单选题连续变量x服从正态分布N(μ,σ2),当变动σ,而μ不变时,正态分布的曲线会()A改变中心,也改变曲线的形状B不改变中心,改变曲线的形状C改变中心,不改变曲线的形状D不改变中心,也不改变曲线的形状
多选题设x~N(0,1),则下列各式成立的有( )。AP(Xa)=P(X≥a)=φ(a)BP(a≤X≤b)=φ(b)-φ(a)CP(|X|≤a)=2φ(a)-1Dφ(-a)=-φ(a)Eφ(-a)=2φ(a)br /span/span
多选题设X~N(0,1),则下列各式成立的有( )。AP(Xa)=P(X≥a)=φ(a)BP(a≤X≤b)=φ(b)-φ(a)CP(|X|≤a)=2φ(a)-1Dφ(-a)=-φ(a)Eφ(-a)=2 φ(a)