阅读以下说明和流程图，从供选择的答案中选出应填入流程图(n)处的字句写在答题纸的对应栏内。【说明】一个印刷电路板的布线区域可分成n×m个方格，如图3-1(a)所示，现在需要确定电路板中给定的两个方格的中心点之间的最短布线方案。电路只能沿水平或垂直方向布线，如图3-1(b)中虚线所示。为了避免线路相交，应将已布过线的方格做封锁标记，其他线路不允许穿过被封锁的方格。设给定印刷电路板的起始方格x与目的方格y尚未布线，求这两个方格间最短布线方案的基本思路是：从起始方格x开始，先考查距离起始方格距离为1的可达方格并用一个路径长度值标记，然后依次考查距离为2，3，…的可达方格，直到距离为k的某一个可达方格就是目标方格y时为止，或者由于不存在从x到y的布线方案而终止。布线区域中的每一个方格与其相邻的上、下、左、右四个方格之间的距离为1，依次沿下、右、上、左这四个方向考查，并用一个队列记录可达方格的位置。表3-1给出了沿这四个方向前进1步时相对于当前方格的相对偏移量。例如，设印刷电路板的布线区域可划分为一个6×8的方格阵列，如图3-2(a)所示，其中阴影表示已封锁方格。从起始方格x(位置[3，2]，标记为0)出发，按照下、右、上、左的方向依次考查，所标记的可达方格如图3-2(a)所示，目标方格为y(位置[4，7]，标记为10)，相应的最短布线路径如图3-2(b)虚线所示。【图3-2】图3-3和图3-4所示的流程图即利用上述思路，在电路板方格阵列中进行标记，图中使用的主要符号如表3-2所示。在图3-4中，设置电路板初始格局即将可布线方格置为数值-1、已布线方格(即封锁方格)置为-9。设置方格阵列“围墙”的目的是省略方格位置的边界条件判定，方法是在四周附加方格，并将其标记为-9(与封锁标记相同)。供选择的答案A．Found≠true B．Found=trueC．T=EndPos D．Q．insert(T)E．T←Q.delete() F．CurPos=EndPosG．i≥4 H．CurPos←Q．delete()I．Grid[T.row,T.col]=-1 J．Grid[T.row,T.col]≠-1
阅读以下说明和流程图，从供选择的答案中选出应填入流程图(n)处的字句写在答题纸的对应栏内。
【说明】
一个印刷电路板的布线区域可分成n×m个方格，如图3-1(a)所示，现在需要确定电路板中给定的两个方格的中心点之间的最短布线方案。电路只能沿水平或垂直方向布线，如图3-1(b)中虚线所示。为了避免线路相交，应将已布过线的方格做封锁标记，其他线路不允许穿过被封锁的方格。
设给定印刷电路板的起始方格x与目的方格y尚未布线，求这两个方格间最短布线方案的基本思路是：从起始方格x开始，先考查距离起始方格距离为1的可达方格并用一个路径长度值标记，然后依次考查距离为2，3，…的可达方格，直到距离为k的某一个可达方格就是目标方格y时为止，或者由于不存在从x到y的布线方案而终止。布线区域中的每一个方格与其相邻的上、下、左、右四个方格之间的距离为1，依次沿下、右、上、左这四个方向考查，并用一个队列记录可达方格的位置。表3-1给出了沿这四个方向前进1步时相对于当前方格的相对偏移量。
例如，设印刷电路板的布线区域可划分为一个6×8的方格阵列，如图3-2(a)所示，其中阴影表示已封锁方格。从起始方格x(位置[3，2]，标记为0)出发，按照下、右、上、左的方向依次考查，所标记的可达方格如图3-2(a)所示，目标方格为y(位置[4，7]，标记为10)，相应的最短布线路径如图3-2(b)虚线所示。
【图3-2】
图3-3和图3-4所示的流程图即利用上述思路，在电路板方格阵列中进行标记，图
中使用的主要符号如表3-2所示。在图3-4中，设置电路板初始格局即将可布线方格置为数值-1、已布线方格(即封锁方格)置为-9。设置方格阵列“围墙”的目的是省略方格位置的边界条件判定，方法是在四周附加方格，并将其标记为-9(与封锁标记相同)。
供选择的答案
A．Found≠true B．Found=true
C．T=EndPos D．Q．insert(T)
E．T←Q.delete() F．CurPos=EndPos
G．i≥4 H．CurPos←Q．delete()
I．Grid[T.row,T.col]=-1 J．Grid[T.row,T.col]≠-1
相关考题：
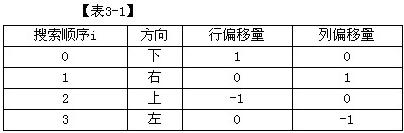
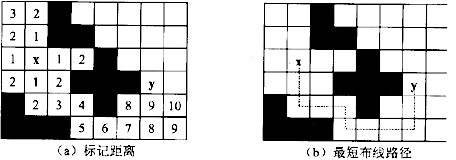
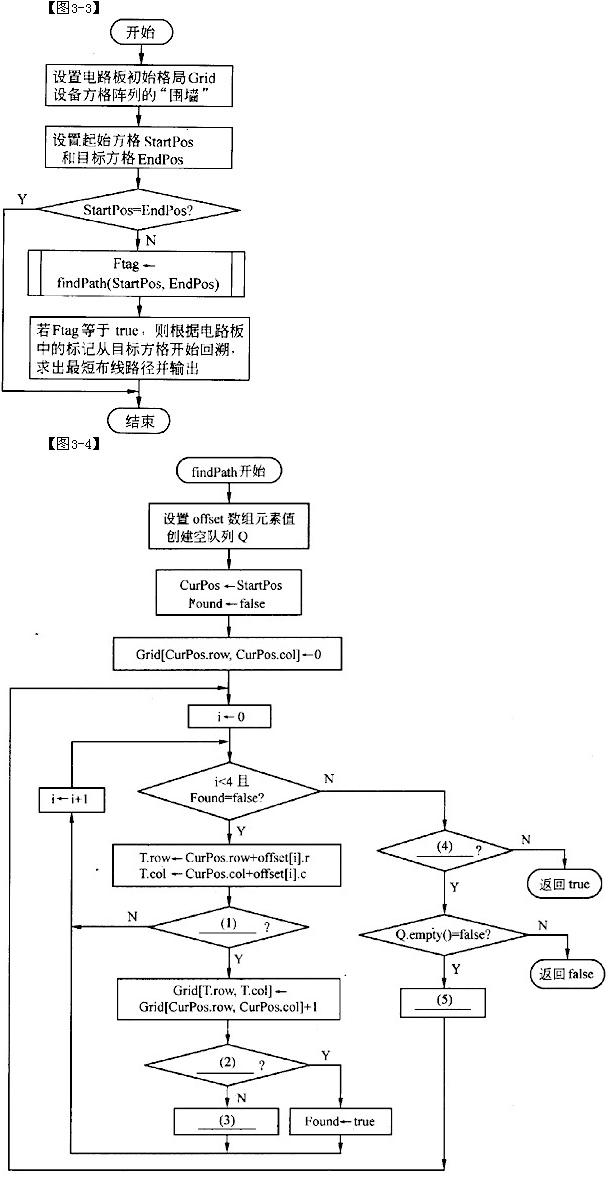
阅读下列说明和流程图，将应填入(n)处的语句写在对应栏内。【说明】下列流程图用于从数组K中找出一切满足：K(I)+K(J)=M的元素对(K(I)，K(J))(1≤I≤J≤N)。假定数组K中的N个不同的整数已按从小到大的顺序排列，M是给定的常数。【流程图】此流程图1中，比较“K(I)+K(J):M”最少执行次数约为(5)。
阅读以下说明和流程图，将应填入(n)处的字句写在对应栏内。【说明】已知头指针分别为La和lb的有序单链表，其数据元素都是按值非递减排列。现要归并La和Lb得到单链表Lc，使得Lc中的元素按值非递减排列。程序流程图如下所示：
阅读以下说明和流程图，将应填入(n)处的字句写在对应栏内。[说明]设学生某次考试的成绩按学号顺序逐行存放于某文件中，文件以单行句点“.”为结束符。下面的流程图读取该文件，统计出全部成绩中的最高分max和最低分min。
阅读下列说明和流程图，将应填入(n)的字句写在对应栏内。【说明】下列流程图(如图4所示)用泰勒(Taylor)展开式sinx=x-x3/3!+x5/5!-x7/7!+…+(-1)n×x2n+1/(2n+1)!+…【流程图】计算并打印sinx的近似值。其中用ε(＞0)表示误差要求。
阅读下列说明和流程图，将应填入(n)处的语句写在对应栏内。【说明】下列流程图用泰勒(Taylor)展开式y=ex=1+x+x2/2!+x3/3!+…+xn/n!+…计算并打印ex的近似值，其中用ε(＞0)表示误差要求。【流程图】
阅读以下说明和流程图，将应填入(n)处的字句写在对应栏内。[说明]下面的流程图实现了正整数序列{K(1),K(2),…,K(n)}的重排，得到的新序列中，比K(1)小的数都在K(1)的左侧，比K(1)大的数都在K(1)的右侧。以n=6为例，序列{12，2，9，13，21，8}的重排过程为：{12,2,9,13,21,8}→{2,12,9,13,21,8}→{9,2,12,13,21,8}→{8,9,2,12,13,21}[流程图]
阅读以下说明和流程图，回答问题1-2，将解答填入对应的解答栏内。[说明]下面的流程图采用欧几里得算法，实现了计算两正整数最大公约数的功能。给定正整数m和 n，假定m大于等于n，算法的主要步骤为：(1)以n除m并令r为所得的余数；(2)若r等于0，算法结束；n即为所求；(3)将n和r分别赋给m和n，返回步骤(1)。[流程图][问题1] 将流程图中的(1)～(4)处补充完整。[问题2] 若输入的m和n分别为27和21，则A中循环体被执行的次数是(5)。
阅读以下说明和流程图，将应填入(n)处的字句写在对应栏内。[说明]下面的流程图用于计算一个英文句子中最长单词的长度(即单词中字母个数)MAX。假设该英文句子中只含字母、空格和句点“.”，其中句点表示结尾，空格之间连续的字母串称为单词。[流程图]
阅读以下说明和流程图，回答问题，并将解答填入对应栏内。【说明】求解约瑟夫环问题。算法分析：n个士兵围成一圈，给他们依次编号，班长指定从第w个士兵开始报数，报到第s个士兵出列，依次重复下去，直至所有士兵都出列。【流程图】【问题】将流程图中的(1)～(5)处补充完整。
阅读下列说明和流程图，将应填入(n)处的语句写在对应栏内。【说明】设学生(学生数少于50人)某次考试的成绩按学号顺序逐行存放于某文件中，文件以单行句点“.”为结束符。下面的流程图用于读取该文件，并把全部成绩从高到低排序到数组B[50]中。【流程图】
?????? 阅读以下说明和流程图，填补流程图中的空缺(1)～(5)，将解答填入答题纸的对应栏内。【说明】本流程图旨在统计一本电子书中各个关键词出现的次数。假设已经对该书从头到尾依次分离出各个关键词{A(i)li=l，…，n}(n＞1)}．其中包含了很多重复项，经下面的流程处理后，从中挑选出所有不同的关键词共m个{K（j）[j=l，…，m}，而每个关键词K（j）出现的次数为NK（j）．j=l，…，m。??????
●试题一阅读下列说明和流程图，将应填入(n)的字句写在答题纸的对应栏内。【说明】下列流程图(如图4所示)用泰勒(Taylor)展开式sinx=x-x3／3!+x5／5!-x7／7!+…+(-1)n×x 2n+1／(2n+1)!+…【流程图】图4计算并打印sinx的近似值。其中用ε(0)表示误差要求。
●试题一阅读下列说明和流程图，将应填入(n)处的语句写在答题纸的对应栏内。【说明】下列流程图用于从数组K中找出一切满足：K(I)+K(J)=M的元素对(K(I)，K(J))(1≤I≤J≤N)。假定数组K中的N个不同的整数已按从小到大的顺序排列，M是给定的常数。【流程图】此流程图1中，比较"K(I)+K(J)∶M"最少执行次数约为 (5) 。图1
阅读下列说明和C++-代码，将应填入（n）处的字句写在答题纸的对应栏内。 【说明】 某发票（lnvoice）由抬头（Head）部分、正文部分和脚注（Foot）部分构成。现采用装饰（Decorator）模式实现打印发票的功能，得到如图5-1所示的类图。【C++代码】 #include using namespace std； class invoice{ public： （1）{ cout
阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。[说明]本流程图旨在统计一本电子书中各个关键词出现的次数。假设已经对该书从头到尾依次分离出各个关键词{A(i)|i=1,…,n}(n＞1)}，其中包含了很多重复项，经下面的流程处理后，从中挑选出所有不同的关键词共m个{K(j)|j=1,…,m}，而每个关键词K(j)出现的次数为NK(j),j=1,…,m。[流程图]
阅读说明和流程图，填补流程图中的空缺（1）?（5），将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1，a2=1，…,an=an-1+an-2!n=3,4,…}的前n项（n>=2) 之和S。例如，菲波那契数列前6项之和为20。计算过程中，当前项之前的两项分别动态地保存在变量A和B中。【流程图】
第一题 阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。【说明】对于大于1的正整数n，(x+1)n可展开为问题：1.1 【流程图】注：循环开始框内应给出循环控制变量的初值和终值，默认递增值为1。格式为：循环控制变量=初值，终值，递增值。
阅读以下说明和流程图，将应填入（n）处的字句写在答题纸的对应栏内。【说明】 下面的流程图旨在统计指定关键词在某一篇文章中出现的次数。设这篇文章由字符A(0)，…，A(n-1)依次组成，指定关键词由字符B(0)，…，B(m-1)依次组成，其中n>m≥1。注意，关键词的各次出现不允许有交叉重叠。例如，在"aaaa"中只出现两次"aa"。该流程图采用的算法是：在字符串A中，从左到右寻找与字符串B相匹配的并且没有交叉重叠的所有子串。流程图中，i 为字符串 A 中当前正在进行比较的动态子串首字符的下标，j为字符串B的下标，k为指定关键词出现的次数。【流程图】
阅读下列说明和C++代码，回答问题，将解答填入答题纸的对应栏内。【说明】某航空公司的会员积分系统将其会员划分为:普卡 (Basic)、银卡(Silver)和金卡 (Gold) 三个等级。非会员 (NonMember) 可以申请成为普卡会员。会员的等级根据其一年内累积 的里程数进行调整。描述会员等级调整的状态图如图 5-1 所示。现采用状态 (State) 模式实现上述场景，得到如图 5-2 所示的类图。【问题1】（15分）阅读上述说明和C++代码，将应填入 (n) 处的字句写在答题纸的对应栏内。
阅读下列说明和 Java 代码，将应填入（n）处的字句写在答题纸的对应栏内。 【说明】 某软件公司欲开发一款汽车竞速类游戏，需要模拟长轮胎和短轮胎急刹车时在路面上 留 下的不同痕迹，并考虑后续能模拟更多种轮胎急刹车时的痕迹。现采用策略（Strategy） 设 计模式来实现该需求，所设计的类图如图 5-1 所示。
阅读下列说明和Java代码，将应填入（n）处的字句写在答题纸的对应栏内。【说明】 某文件管理系统中定义了类OfficeDoc和DocExplorer，当类OfficeDoc发生变化时，类DocExplorer的所有对象都要更新其自身的状态，现采用观察者（Observer）设计模式来实现该需求，所设计的类图如图6-1所示。
阅读下列说明和?C++代码，将应填入(n)处的字句写在答题纸的对应栏内。【说明】阅读下列说明和?Java代码，将应填入?(n)?处的字句写在答题纸的对应栏内。【说明】某快餐厅主要制作并出售儿童套餐，一般包括主餐(各类比萨)、饮料和玩具，其餐品种类可能不同，但其制作过程相同。前台服务员?(Waiter)?调度厨师制作套餐。现采用生成器?(Builder)?模式实现制作过程，得到如图?6-1?所示的类图。