阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。【说明】下列流程图用泰勒(Taylor)展开式y=ex=1+x+x2/2!+x3/3!+…+xn/n!+…计算并打印ex的近似值,其中用ε(>0)表示误差要求。【流程图】
阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。
【说明】
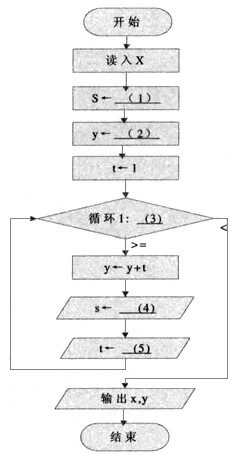
下列流程图用泰勒(Taylor)展开式y=ex=1+x+x2/2!+x3/3!+…+xn/n!+…计算并打印ex的近似值,其中用ε(>0)表示误差要求。
【流程图】
相关考题:
阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。【说明】下列流程图用于从数组K中找出一切满足:K(I)+K(J)=M的元素对(K(I),K(J))(1≤I≤J≤N)。假定数组K中的N个不同的整数已按从小到大的顺序排列,M是给定的常数。【流程图】此流程图1中,比较“K(I)+K(J):M”最少执行次数约为(5)。
阅读以下说明和流程图,回答问题1~2,将解答填入对应的解答栏内。[说明]下面的流程图描述了计算自然数1到N(N≥1)之和的过程。[流程图][问题1] 将流程图中的(1)~(3)处补充完整。[问题2] 为使流程图能计算并输出1*3+2*4+…+N*(N+2)的值,A框内应填写(4);为使流程图能计算并输出不大于N的全体奇数之和,B框内应填写(5)。
阅读下列说明和流程图,将应填入(n)的字句写在对应栏内。【说明】下列流程图(如图4所示)用泰勒(Taylor)展开式sinx=x-x3/3!+x5/5!-x7/7!+…+(-1)n×x2n+1/(2n+1)!+…【流程图】计算并打印sinx的近似值。其中用ε(>0)表示误差要求。
阅读以下说明和流程图,填补流程图中的空缺(1)一(5),将解答填入答题纸的对应栏内。【说明】下面的流程图采用公式ex=1+x+x2/2 1+x3/3 1+x4/4 1+…+xn/n!+???计算ex的近似值。设x位于区间(0,1),该流程图的算法要点是逐步累积计算每项xx/n!的值(作为T),再逐步累加T值得到所需的结果s。当T值小于10-5时,结束计算。【流程图】
阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。【说明】有数组A(4,4),把1到16个整数分别按顺序放入A(1,1),…,A(1,4),A(2,1),…,A(2,4),A(3,1),…,A(3,4),A(4,1),…,A(4,4)中,下面的流程图用来获取数据并求出两条对角线元素之积。【流程图】
阅读以下说明和流程图,将应填入(n)处的字句写在对应栏内。[说明]下面的流程图用于计算一个英文句子中最长单词的长度(即单词中字母个数)MAX。假设该英文句子中只含字母、空格和句点“.”,其中句点表示结尾,空格之间连续的字母串称为单词。[流程图]
阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。【说明】设学生(学生数少于50人)某次考试的成绩按学号顺序逐行存放于某文件中,文件以单行句点“.”为结束符。下面的流程图用于读取该文件,并把全部成绩从高到低排序到数组B[50]中。【流程图】
●试题一阅读下列说明和流程图,将应填入(n)的字句写在答题纸的对应栏内。【说明】下列流程图(如图4所示)用泰勒(Taylor)展开式sinx=x-x3/3!+x5/5!-x7/7!+…+(-1)n×x 2n+1/(2n+1)!+…【流程图】图4计算并打印sinx的近似值。其中用ε(0)表示误差要求。
●试题一阅读下列说明和流程图,将应填入(n)处的语句写在答题纸的对应栏内。【说明】下列流程图用于从数组K中找出一切满足:K(I)+K(J)=M的元素对(K(I),K(J))(1≤I≤J≤N)。假定数组K中的N个不同的整数已按从小到大的顺序排列,M是给定的常数。【流程图】此流程图1中,比较"K(I)+K(J)∶M"最少执行次数约为 (5) 。图1