图示钢制竖直杆DB与水平杆AC刚接于B,A端固定,P、l、a与圆截面杆直径d为已知。按第三强度理论,相当应力σr3为:
图示钢制竖直杆DB与水平杆AC刚接于B,A端固定,P、l、a与圆截面杆直径d为已知。按第三强度理论,相当应力σr3为:

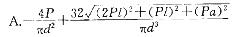


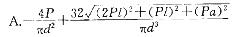

参考解析
解析:提示:这是压缩、双向弯曲和扭转的组合变形问题,危险点在A截面的右下部。
相关考题:
如图所示,直径为d的圆截面杆AB,在B端受一力偶m=Pd/2(力偶作用面与杆轴垂直)及一偏心力P(与杆轴平行)的作用。材料弹性模量为E,横向变形系数(泊松比)μ=1/3。试求圆柱表面沿母线Oa及与母线成45°的Ob方向上的线应变εa和εb值。
图所示圆截面杆件d=80mm,长度l=1000mm,承受轴向力F1=30kN,横向力F2=1.2kN,外力偶M=700N·m的作用,材料的许用应力[σ]=40MPa,试求:①作杆件内力图。②按第三强度理论校核杆的强度。
应用杆件强度条件公式N/A≤[σ](式中N为杆件计算截面上的内力,A为杆件计算截面的面积,[σ]为杆件材料的许用应力),可以用来( )。A.校核杆件的刚度 B.校核杆件的强度 C.设计杆件的截面尺寸 D.计算杆件的许可荷载 E.计算杆件的纵向弯曲度
已知圆截面杆扭转时,横截面上的最大剪应力为τmax,两端面间的相对扭转角为φ。若圆杆的直径增大一倍(即为原直径的两倍),则此时的最大剪应力τmax和相对扭 转角φ与原来的τmax和φ的比值为( )。A.τmax/τmax=1/2,φ/φ=1/4B.τmax/τmax=1/4,φ/φ=1/8C.τmax/τmax=1/8,φ/φ=1/8D.τmax/τmax=1/8,φ/φ=1/16
图示刚梁AB由杆1和杆2支承,已知两杆的材料相同,长度不等,横截面面积分别为A1和A2,若载荷P使刚梁平行下移,则其横截面面积:(A)A1<A2(B)A1=A2(C)A1>A2(D)A1、A2为任意
如图所示结构中,AB段为圆截面杆,直径d=80mm,A端固定,B端为球铰连接,BC段为正方形截面杆,边长a=70mm,C端亦为球铰连接,两杆材料相同,弹性模量E=206GPa,比例极限σp=20MPa,l=3m,稳定安全系数nst=2. 5,则结构的许可荷载[P]为:A. [P] = 165kN B. [P] = 181kNC. [P]=420kN- D. [P]=346kN
等截面直杆受轴向拉力F作用而产生弹性伸长,已知杆长为l,横截面面积为A,材料弹性模量为E,泊松比为v。根据拉伸理论,影响该杆横截面上应力的因素为()。 A. E, v, F B. l,A,F C. l, A, E, v, F D. A, F
单选题材料相同、横截面面积相等的两拉杆,一为圆形截面,另一为方形截面,在相同拉力作用下,两拉杆横截面上的应力()。A相等B圆杆大于方杆C方杆大于圆杆D长杆大于短杆