按照马柯威茨的描述，下面的资产组合中哪个不会落在有效边界上（　　）A、只有资产组合W不会落在有效边界上B、只有资产组合X不会落在有效边界上C、只有资产组合Y不会落在有效边界上D、只有资产组合Z不会落在有效边界上

按照马柯威茨的描述，下面的资产组合中哪个不会落在有效边界上（　　）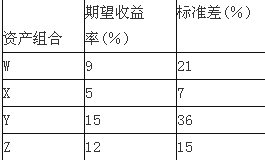

A、只有资产组合W不会落在有效边界上
B、只有资产组合X不会落在有效边界上
C、只有资产组合Y不会落在有效边界上
D、只有资产组合Z不会落在有效边界上

参考解析

解析：2组合相对于W组合来讲，期望收益可以增加，而风险降低，使得W组合不会落在有效边界上。

相关考题：

马柯威茨均值方差模型主要应用于资金在各种证券资产上的合理分配。 （ ）
查看答案
投资组合理论为投资者提供了如何确定最优资产组合的方法和行动指南，而APT模型则回答了假定所有的投资者均按照马柯威茨模型构建组合并在有效前沿上投资的证券定价问题。 （ ）
查看答案
马柯威茨的投资组合理论确定了风险资产组合的有效边界与市场投资组合的关系。( )
查看答案
理性投资者只需在有效边界上选择证券组合是马柯威茨均值－方差模型的结论。（ ）
查看答案
有效边界是马柯维茨证券组合可行集左上方边界的曲线,又称有效集或有效组合。() 此题为判断题(对，错)。
查看答案
资本资产定价模型与马柯威茨证券组合理论相比其最大优点是可以检验。 （ ）
查看答案
在马柯威茨均值方差模型中，投资者的偏好无差异曲线与有效边界的切点（ ）。A．是投资者的最优组合B．是最小方差组合C．是市场组合D．是具有低风险和高收益特征的组合
查看答案
马柯威茨的假设条件明确描述了下述情况的两种组合A和B之间的优劣。
查看答案
（ ）年，马柯威茨的学生威廉·夏普提出旨在简化马柯威茨组合理论实际应用的“单因素模型”。A．1953B．1963C．1954D．1964
查看答案
在马柯威茨均值方差模型中，可行域的左边界可能出现凹陷。（ ）
查看答案
按照马柯维茨的描述，表3-2中的资产组合中不会落在有效边界上的是()。A:只有资产组合W不会落在有效边界上B:只有资产组合X不会落在有效边界上C:只有资产组合Y不会落在有效边界上D:只有资产组合Z不会落在有效边界上
查看答案
在马柯威茨均值方差模型中，投资者的偏好无差异曲线与有效边界的切点()。A:是投资者的最优组合B:是最小方差组合C:是市场组合D:是具有低风险和高收益特征的组合
查看答案
按照马柯威茨的描述，下面的资产组合中不会落在有效边界上的是（ ）。A.只有资产组合W不会落在有效边界上B.只有资产组合X不会落在有效边界上 C.只有资产组合Y不会落在有效边界上 D.只有资产组合Z不会落在有效边界上
查看答案
按照马克维茨的描述，下面的（ ）资产组合不会落在有效边界上。A.WB.XC.YD.Z
查看答案
根据马克维茨的描述，图中的（ ）资产组合不会落在有效边界上A.WB.XC.YD.Z
查看答案
理性投资者只需在有效边界上选择证券组合，这是马柯威茨均值一方差模型的结论。()
查看答案
在马柯威茨模型的有效边界上有两个组合A与B，组合A期望收益大于组合B的期望收益，则组合A—定优于组合B。()
查看答案
马柯威茨的投资组合理论的主要贡献表现在（）。A:创立了以均值与方差为基础进行证券分析与组合构造的理论B:降低了构造有效投资组合的计算复杂性与所费时间C:以因素模型解释了资本资产的定价问题D:确立了市场投资组合与有效边界的相对关系
查看答案
资产组合理论的提出者是()。A:哈里·马柯威茨B:威廉·夏普C:斯蒂芬·罗斯D:尤金·法玛
查看答案
有效市场理论下的有效市场概念指的是信息有效，它既不同于通常所指的资源有效配置的帕雷托有效，也不同于马柯威茨关于组合均值方差有效组合的概念。()
查看答案
按照马柯维茨的描述，表5—2中的资产组合中不会落在有效边界上的是( )。表5—2资产组合表A.只有资产组合W不会落在有效边界上B.只有资产组合X不会落在有效边界上C.只有资产组合Y不会落在有效边界上D.只有资产组合Z不会落在有效边界上
查看答案
按照马柯维茨的描述，表 中的资产组合中不会落在有效边界上的是(　　)。A.只有资产组合W不会落在有效边界上B.只有资产组合x不会落在有效边界上C.只有资产组合Y不会落在有效边界上D.只有资产组合z不会落在有效边界上
查看答案
现代证券组合理论包括（）。A、马柯威茨的均值方差模型B、单因素模型C、资本资产定价模型D、套利定价理论
查看答案
马柯威茨关于投资组合的奠基之作是（）A、均值方差模型B、证券组合的选择C、资本定价模型D、论有效边界
查看答案
当引入无风险借贷后，有效边界的范围为（）。A、仍为原来的马柯维茨有效边界B、从无风险资产出发到T点的直线段C、从无风险资产出发到T点的直线段加原马柯维茨有效边界在T点上方的部分D、从无风险资产出发与原马柯维茨有效边界相切的射线
查看答案
单选题马柯威茨关于投资组合的奠基之作是（）A均值方差模型B证券组合的选择C资本定价模型D论有效边界
查看答案
单选题当引入无风险借贷后，有效边界的范围为（）。A仍为原来的马柯维茨有效边界B从无风险资产出发到T点的直线段C从无风险资产出发到T点的直线段加原马柯维茨有效边界在T点上方的部分D从无风险资产出发与原马柯维茨有效边界相切的射线
查看答案
热门标签