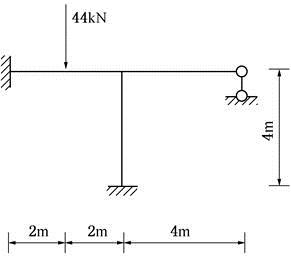
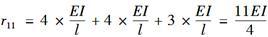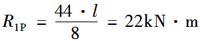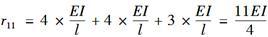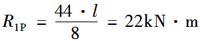图示结构,各柱EI=常数,用位移法计算时,基本未知量数目是()A.2B.4C.6D.8
图示结构各杆EI=常数,用力矩分配法计算的分配系数μBC=1/2。()此题为判断题(对,错)。
图所示中,用力法解图(a)所示结构(图中kM为弹性铰支座A的转动刚度系数),取图(b)所示的力法基本体系,力法典型方程为( )。
图所示的刚架,EI=常数,各杆长为l,A截面的转角为( )。
图所示结构各杆温度均升高t℃,且已知EI和EA均为常数,线膨胀系数为α,则点D的竖向位移△Dn为( )。 A、-αta B、αta C、0 D、2αta
用力法求解图示结构(EI=常数),基本体系及基本未知量如图所示,力法方程中系数△1P为:
位移法方程中的系数和自由项的物理意义是( )。A、系数—位移;自由项—力B、系数—力;自由项—位移C、都是位移D、都是力
用位移法计算图示结构,已知典型方程的系数r11=27EI/l3,R1P=-F/2,各柱EI=常数,右柱底的弯矩为( )。A.-Fl/8B.-Fl/9C.Fl/8D.Fl/9
如图所示组合结构,梁式杆件EI=常数,桁架杆件EA=常数,C点竖向位移为( )。 A、向上 B、向下 C、为零 D、需计算确定
图所示结构,EI=常数,截面高h=常数,线膨胀系数为α,外侧环境温度降低t℃,内侧环境温度升高t℃,引起的C点竖向位移大小为( )。
用位移法计算图结构时,附加刚臂的约束反力矩R1P之值为( )kN·m。 A、-38 B、-28 C、26 D、32
用力法求解图所示结构(EI=常数),基本体系及基本未知量如图所示,力法方程中的系数为( )。
图示各结构中,除特殊注明者外,各杆EI=常数。其中不能直接用力矩分配法计算的结构是:
图所示结构,各杆,当支座B发生图示的移动时,结点E的水平位移为( )。
用位移法计算图所示梁(EI=常数),基本体系如图所示,k11为( )。 A、6EI/l B、7EI/l C、8EI/l D、9EI/l
图示结构当釆用位移法计算时,刚度系数k11(r11)等于:
如图a)所示结构,取图b)为力法基本体系,EI=常数,Δ1P为:
图示结构各杆EI=常数,其C端的水平位移(→)为:
用位移法计算图示连续梁,并绘出弯矩图。各杆EI相同且为常数。
用力矩分配法计算图示结构,并绘出弯矩图。各杆EI相同且为常数。
用力法计算图示结构,并作弯矩图。各杆EI相同且为常数。
用位移法求解刚架,并绘弯矩图。各杆EI相同等于常数。
在位移法的基本方程中()与载荷无关,为结构常数。A、主系数和副系数B、主系数和自由项C、副系数和自由项D、自由项
判断题力法典型方程中全部系数和自由项都是基本结构的位移,所以,求系数和自由项的实质就是求静定结构的位移。A对B错
单选题在位移法的基本方程中()与载荷无关,为结构常数。A主系数和副系数B主系数和自由项C副系数和自由项D自由项