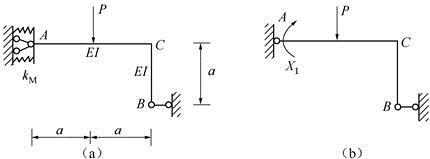
图所示中,用力法解图(a)所示结构(图中kM为弹性铰支座A的转动刚度系数),取图(b)所示的力法基本体系,力法典型方程为( )。
图所示中,用力法解图(a)所示结构(图中kM为弹性铰支座A的转动刚度系数),取图(b)所示的力法基本体系,力法典型方程为( )。
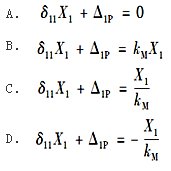

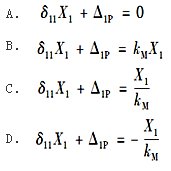
参考解析
解析:该结构为一次超静定结构,建立力法典型方程得δ11X1+Δ1P=Δ1,力法典型方程是变形协调方程,因此方程右端的Δ1表示原超静定结构沿X1方向的给定位移。在图(b)所示力法基本体系中,Δ1表示截面A的转角,


相关考题:
悬臂梁的自由端作用横向力P,若各梁的横截面分别如图a)~h)所示,该力P的作用线为各图中的虚线,则梁发生平面弯曲的是:A.图a)、图g)所示截面梁B.图c)、图e)所示截面梁C.图b)、图d)所示截面D.图f)、图h)所示截面
如图a所示桁架,EA为常数,取图b为力法基本体系,则力法方程系数间的关系为( )。 A、δ22<δ11,δ12>0 B、δ22>δ11,δ12>0 C、δ22<δ11,δ12<0 D、δ22>δ11,δ12<0
图a)所示桁架,EA=常数,取图b)为力法基本体系,则力法方程系数间的关系为:A. δ2211,δ12>0 B.δ22>δ11,δ12>0C. δ2211,δ1222>δ11,δ12