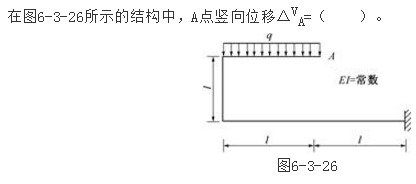
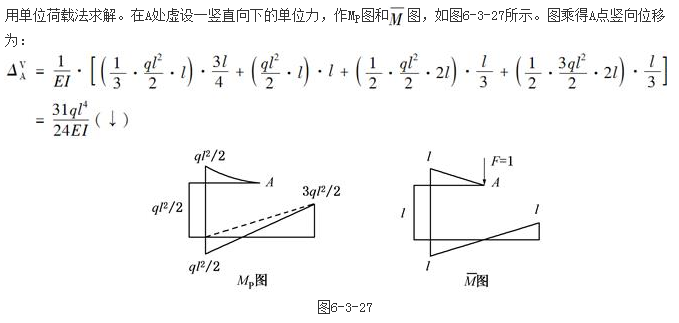
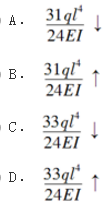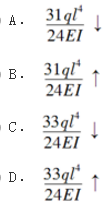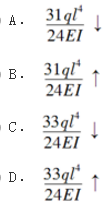图所示刚架,各杆线刚度相同,则结点A的转角大小为( )。
图所示结构各杆温度均升高t℃,且已知EI和EA均为常数,线膨胀系数为α,则点D的竖向位移△Dn为( )。 A、-αta B、αta C、0 D、2αta
图示结构杆长为l,EI=常数,C点两侧截面相对转角φC为:
图所示的结构AB,杆件A截面的转角θA值为( )。
已知刚架的弯矩图如图所示,杆的抗弯刚度为杆的为2EI,则结点B的角位移等于:
图示刚架,各杆线刚度相同,则结点A的转角大小为( )。
图所示刚架,EI=常数,结点A的转角是( )。(提示:利用转动刚度的概念)
如图所示的结构,EI=常数,杆端弯矩(顺时针为正)正确的是( )。
图示刚架,EI为常数,结点A的转角是( )。(提示:利用对称性和转动刚度的概念)
图示刚架EI=常数,截面C和D的相对转角为( )。
图示刚架,EI为常数,忽略轴向变形。当D支座发生支座沉降时,B点转角为( )。
图示两刚架的EI均为常数,已知EIa=4EIb,则图a)刚架各截面弯矩与图b)刚架各相应截面弯矩的倍数关系为:
所示刚架支座A下移量为a,转角为α则B端竖向位移( )。 A、与h、l、El均有关 B、与h、l有关,与El无关 C、与l有关,与h、El均无关 D、与EI有关,与h、l均无关
图示刚架,EI=常数,结点A的转角是( )。(提示:利用转动刚度的概念)
图所示梁AB,EI为常数,固支端A发生顺时针的支座转动θ,由此引起的B处的转角为( )。{图} A.θ,顺时针 B.θ,逆时针 C.θ/ 2,顺时针 D.θ/ 2,逆时针
图所示刚架,EI为常数,结点A的转角是( )。(提示:利用对称性和转动刚度的概念)
如图所示的刚架,各杆EI相同,C点竖向位移(向下为正)等于( )。
图示为刚架在均布荷载作用下的M图,曲线为二次抛物线,横梁的抗弯刚度为2EI,竖柱为EI,支座A处截面转角为:
图式刚架,各杆线刚度i相同,则结点A的转角大小为:
用位移法计算图所示梁(EI=常数),基本体系如图所示,k11为( )。 A、6EI/l B、7EI/l C、8EI/l D、9EI/l
图示为结构在荷载作用下的M图,各杆EI=常数,则支座B处截面的转角为:
图示结构各杆EI=常数,其C端的水平位移(→)为:
用力法计算图示结构,并作弯矩图。各杆EI相同且为常数。
用位移法求解刚架,并绘弯矩图。各杆EI相同等于常数。