某工程时标网络图如下图所示，则工作A的自由时差为（ ）。A：0B：1C：2D：3
图所示中，用力法解图（a）所示结构（图中kM为弹性铰支座A的转动刚度系数），取图（b）所示的力法基本体系，力法典型方程为（ ）。
如图a)所示结构，若将链杆撤去，取图b)为力法基本体系，则力法方程及知分别为:
图b)是图a)结构的力法基本体系，则力法方程中的系数和自由项为：A.Δ1P>0, δ121P121P>0, δ12>0 D. Δ1P12>0
用力法求解图示结构(EI=常数），基本体系及基本未知量如图所示，力法方程中系数△1P为：
用力法计算图（a）所示结构，取基本结构如图（b）所示，其中系数δ11为（ ）。
如图a)所示结构，EI=常数，取图b)为力法基本体系，则下述结果中错误的是: A.δ23=0B. δ31=0C.Δ2P=0D.δ12=0
图所示为两次超静定结构，下列图中作为力法的基本结构求解过程最简便的是（ ）。 A、A B、B C、C D、D
如图a所示桁架，EA为常数，取图b为力法基本体系，则力法方程系数间的关系为（ ）。 A、δ22＜δ11，δ12＞0 B、δ22＞δ11，δ12＞0 C、δ22＜δ11，δ12＜0 D、δ22＞δ11，δ12＜0
如图所示，用力法且采用图（b）所示的基本体系计算图（a）所示梁，Δ1P为（ ）。
图示结构取图（b）为力法基本体系，EI为常数，下列哪项是错误的？（ ）
如图（a）所示的结构，EI＝常数，取图（b）为力法基本体系，则下列各项错误的是（ ）。 A、δ23＝0 B、δ31＝0 C、Δ2P＝0 D、δ12＝0
用位移法求解图所示结构，独立的基本未知量个数为（ ）。 A、1 B、2 C、3 D、4
用力法求解图所示结构（EI=常数），基本体系及基本未知量如图所示，力法方程中的系数为（ ）。
如图a)所示桁架，EA=常数，取图b)为力法基本体系，则力法方程系数间的关系为：A. δ2211,δ12>0 B.δ22>δ11,δ12>0C. δ2211,δ1222>δ11,δ12
图所示结构取图（b）为力法基本体系，El为常数，下列哪项是错误的[A8] ?（ ）
图a)所示结构，取图b)为力法基本体系，则力法方程中的Δ2C为: A. a+bB. a+lθC. -aD. a
图中，用力法求解图（a）所示结构，取图（b）所示力法基本体系，则力法典型方程δ11X1+Δ1p=0中的Δ1P之值为（ ）。
图示结构支座A下沉了d并发生了顺时针方向转角α，当用力法计算并取图（b）为基本结构时，力法方程应为（ ）。
图所示为超静定桁架的基本结构及多余为知力X=1作用下的各杆内力，EA为常数，则为（ ）。
图a)所示桁架，EA=常数，取图b)为力法基本体系，则力法方程系数间的关系为:A.δ11=δ22,δ12>0 C.δ11≠δ22,δ12>0B.δ11≠δ22,δ1211=δ22,δ12
如图a)所示结构，取图b)为力法基本体系，EI=常数，Δ1P为:
如图a)所示桁架各杆EA均为有限值。当撤去杆AB采用图b)为力法基本体系时，相应力法方程的右端项应：A. >0 B. 1、P2的关系而定
如图a)所示结构，取图b)为力法基本体系，则力法方程中的Δ2C为: A. a+b B. a+lθ C. -a D. a
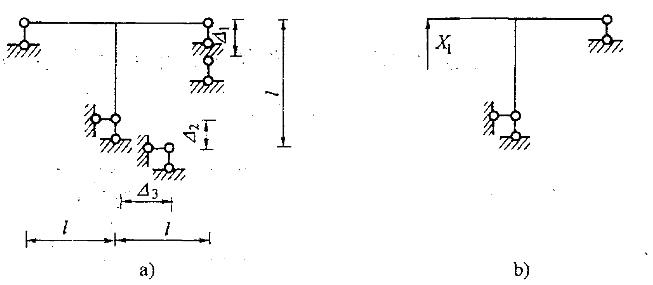
如图a)所示结构，取图b)为力法基本体系，相应力法方程为δ11X1+Δ1C=0，其中Δ1C为：A. Δ1+Δ2B. Δ1+Δ2+Δ3C. 2Δ2-Δ1D. Δ1-2Δ2
图a)所示桁架，EA=常数，取图b)为力法基本体系，则力法方程系数间的关系为：A. δ2211,δ12>0 B.δ22>δ11,δ12>0C. δ2211,δ1222>δ11,δ12
二值图象中分支点的连接数为（）。A、0B、1C、2D、3
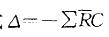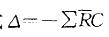求，或根据几何关系分析。