质量为m,长为2l的均质杆初始位于水平位置, 如图所示。A端脱落后,杆绕轴B转动,当杆转到铅垂位置时,AB 杆B处的约束力大小为:
图所示中,用力法解图(a)所示结构(图中kM为弹性铰支座A的转动刚度系数),取图(b)所示的力法基本体系,力法典型方程为( )。
如图a)所示结构,若将链杆撤去,取图b)为力法基本体系,则力法方程及知分别为:
图b)是图a)结构的力法基本体系,则力法方程中的系数和自由项为:A.Δ1P>0, δ121P121P>0, δ12>0 D. Δ1P12>0
用力法求解图示结构(EI=常数),基本体系及基本未知量如图所示,力法方程中系数△1P为:
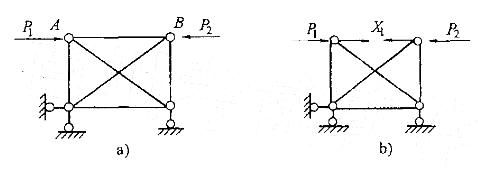
如图a所示桁架,EA为常数,取图b为力法基本体系,则力法方程系数间的关系为( )。 A、δ22<δ11,δ12>0 B、δ22>δ11,δ12>0 C、δ22<δ11,δ12<0 D、δ22>δ11,δ12<0
如图所示,用力法且采用图(b)所示的基本体系计算图(a)所示梁,Δ1P为( )。
如图所示,桁架DE杆的内力为( )。 A、F B、0 C、-F D、-2F
设各杆的EA值相同,在图所示的桁架中,节点C的竖向位移为( )。
如图所示组合结构,梁式杆件EI=常数,桁架杆件EA=常数,C点竖向位移为( )。 A、向上 B、向下 C、为零 D、需计算确定
图a)所示结构,取图b)为力法基本体系,相应力法方程为δ11X1+Δ1C=0,其中Δ1C为:A. Δ1+Δ2B. Δ1+Δ2+Δ3C. 2Δ2-Δ1D. Δ1-2Δ2
用力法求解图所示结构(EI=常数),基本体系及基本未知量如图所示,力法方程中的系数为( )。
如图a)所示桁架,EA=常数,取图b)为力法基本体系,则力法方程系数间的关系为:A. δ2211,δ12>0 B.δ22>δ11,δ12>0C. δ2211,δ1222>δ11,δ12
图中,用力法求解图(a)所示结构,取图(b)所示力法基本体系,则力法典型方程δ11X1+Δ1p=0中的Δ1P之值为( )。
图所示为超静定桁架的基本结构及多余为知力X=1作用下的各杆内力,EA为常数,则为( )。
图a)所示桁架,EA=常数,取图b)为力法基本体系,则力法方程系数间的关系为:A.δ11=δ22,δ12>0 C.δ11≠δ22,δ12>0B.δ11≠δ22,δ1211=δ22,δ12
如图a)所示结构,EI=常数,取图b)为力法基本体系,则下述结果中错误的是: A.δ23=0 B. δ31=0C.Δ2P=0 D.δ12=0
如图a)所示结构,取图b)为力法基本体系,EI=常数,Δ1P为:
图示桁架各杆抗拉刚度均为EA,取B支座反力为力法的基本未知量X1(向左为正),则有:A. X11=0C.X1>0 D.X1方向无法确定
如图a)所示结构,取图b)为力法基本体系,则力法方程中的Δ2C为: A. a+b B. a+lθ C. -a D. a
如图a)所示结构,取图b)为力法基本体系,相应力法方程为δ11X1+Δ1C=0,其中Δ1C为:A. Δ1+Δ2B. Δ1+Δ2+Δ3C. 2Δ2-Δ1D. Δ1-2Δ2
图a)所示桁架,EA=常数,取图b)为力法基本体系,则力法方程系数间的关系为:A. δ2211,δ12>0 B.δ22>δ11,δ12>0C. δ2211,δ1222>δ11,δ12
如图所示,直杆承受P1和P2的作用,若使A点处正应力σA为零,则P1与P2的关系为( )。
A.各杆内力均不为OB.各杆内力均为0C.仅AB杆内力不为0D.仅AB杆内力为0
如图5-9所示等直杆,杆长为3a,材料的拉压刚度为EA,受力如图示。问杆中点横截面的铅垂位移为( )。A.0 B.Fa/EA C.2Fa/EA D.3Fa/EA
如图5-11所示桁架,在节点C处沿水平方向受力F作用。各杆的抗拉刚度相等。若结点C的铅垂位移以sC表示,BC杆的轴力以FNBC表示,正确的为()。A. FNBC= 0, sC= 0 B. FNBC= 0, sC≠ 0 C. FNBC≠ 0, sC= 0 D. FNBC≠ 0, sC≠ 0