某地高校教育经费(x)与高校学生人数(y)连续6年的统计资料如下:要求:(1)建立回归直线方程,估计教育经费为500万元时的在校学生数;(2)计算估计标准误差。
某地高校教育经费(x)与高校学生人数(y)连续6年的统计资料如下:
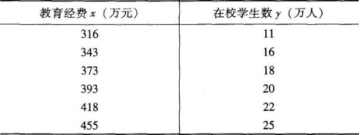
要求:(1)建立回归直线方程,估计教育经费为500万元时的在校学生数;
(2)计算估计标准误差。

要求:(1)建立回归直线方程,估计教育经费为500万元时的在校学生数;
(2)计算估计标准误差。
参考解析
解析:先列出计算表:
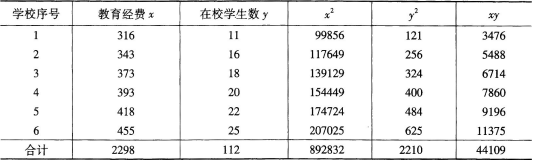
(1)设方程为y=a+bx,则
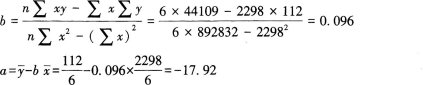
直线回归方程为y=-17.92+0.096x
当x=500时,y=30.08
即教育经费为500万元时,在校生数大约为30.08万人。
(2)根据以上结果可以得出下表:
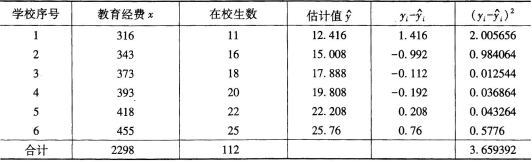
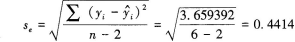
即估计标准误差为0.4414。

(1)设方程为y=a+bx,则
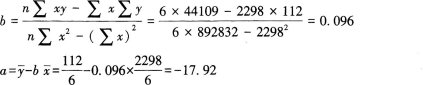
直线回归方程为y=-17.92+0.096x
当x=500时,y=30.08
即教育经费为500万元时,在校生数大约为30.08万人。
(2)根据以上结果可以得出下表:

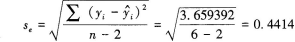
即估计标准误差为0.4414。
相关考题:
流行病学研究发现:某病暴露与两种不同的疾病X和Y有联系。对疾病X的相对危险度为6.0,特异危险度5%;对疾病Y的相对危险度为3.0,特异危险度为20%据此,可以得出如下结论A.暴露与疾病X的联系强度是与疾病Y的联系强度的4倍B.在未暴露者中,发生疾病Y的人数将是发生疾病X的人数的4倍C.消除暴露后,减少的疾病Y的发病人数和减少的疾病X发病人数将不同D.在暴露者中,发生疾病X的人数将是发生疾病Y的人数的1倍E.以上都不是
A={x|x<100且为质数},在A上定义*和.如下:x*y=max(x,y),x.y=LCM(x,y),x,y∈A,这里LCM(x,y)表示x与y的最小公倍数,则下面命题正确的是Ⅰ.<A,*>构成代数系统:Ⅱ.<A,.>构成代数系统;A.只有ⅠB.只有ⅡC.Ⅰ和ⅡD.没有
有如下程序:includemain(){float x=2.0,y; if(x10.0)y=1.0/x; 有如下程序: #include <stdio.h> main() { float x=2.0,y; if(x<0.0) y=0.0; else if(x>10.0) y=1.0/x; else y=1.0; printf("%f/n",y); } 该程序的输出结果是( )。A.0B.0.25C.0.5D.1
有如下程序main(){float x=2.0,y;if(x10.0)y=1.0/x;else y=1.0;printf("%f 有如下程序 main() {float x=2.0,y; if(x<0.0)y=0.0; else if(x>10.0)y=1.0/x; else y=1.0; printf("%f\n",y);} 该程序的输出结果是A.0.000000B.0.250000C.0.500000D.1.000000
有如下程序main(){ float x=2.0,y;if(x10.0)y=1.O/x;else y=1.0;printf("% 有如下程序 main() { float x=2.0,y; if(x<0.0)y=0.0; else if(x>10.0)y=1.O/x; else y=1.0; printf("%f\n",y);} 该程序的输出结果是A.0B.0.25C.0.5D.1
流行病学研究发现某种暴露与两种不同的疾病X和Y有联系。对疾病X的相对危险度为6.0,特异危险度为 5%;对疾病Y的相对危险度为3.0,特异危险度为20%。据此,可以得出如下结论A.暴露与疾病X的联系强度是与疾病 Y的联系强度的4倍B.在未暴露者中,发生疾病Y的人数将是发生疾病X的人数的4倍C.消除暴露后,减少的疾病Y的发病人数和减少的疾病X的发病人数将不同D.在暴露者中,发生疾病X的人数将是发生疾病Y的人数的2倍E.在暴露者中,疾病X的发病率比疾病Y高15%
A={x,x<100且为质数},在A上定义*和.如下: x*y=max(x,y),x.y=LCM(x,y), 这里LCM(x,y)表示x与y的最小公倍数,则下面命题正确的是( )。Ⅰ.<A,*>构成代数系统Ⅱ.<A,.>构成代数系统A.只有ⅠB.只有ⅡC.Ⅰ和ⅡD.没有
A.只能确定一个具有连续偏导数的隐函数z=z(x,y)B.可确定两个具有连续偏导数的隐函数y=y(x,y)和z=z(x,y)C.可确定两个具有连续偏导数的隐函数x=x(x,y)和z=z(x,y)D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)
流行病学研究发现某种暴露与两种不同的疾病X和Y有联系。对疾病X的相对危险度为6.0,特异危险度为5%;对疾病Y的相对危险度为3.0,特异危险度为20%。据此,可以得出如下结论()A、暴露与疾病X的联系强度是与疾病Y的联系强度的4倍B、在未暴露者中,发生疾病Y的人数将是发生疾病X的人数的4倍C、消除暴露后,减少的疾病Y的发病人数和减少的疾病X的发病人数将不同D、在暴露者中,发生疾病X的人数将是发生疾病Y的人数的2倍E、在暴露者中,疾病X的发病率比疾病Y高15%
下列结论正确的是().A、x=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点连续的充分条件B、z=f(x,y)在点(x,y)连续是f(x,y)的偏导数存在的必要条件C、z=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点可微分的充分条件D、z=(x,y)在点(x,y)连续是f(x,y)在该点可微分的必要条件
下列结论正确的是().A、z=f(x,y)在点(x,y)的偏导数存在是f(x,y)在该点连续的充分条件B、z=f(x,y)在点(x,y)连续是f(x,y)的偏导数存在的必要条件C、z=(x,y)在点(x,y)的偏导数存在是f(x,y)在该点可微分的充分条件D、z=(x,y)在点(x,y)连续是f(x,y)在该点可微分的必要条件
单选题以下关于二元函数的连续性的说法正确是( )。A若f(x,y)沿任意直线y=kx在点x=0处连续,则f(x,y)在(0,0)点连续B若f(x,y)在点(x0,y0)点连续,则f(x0,y)在y0点连续,f(x,y0)在x0点连续C若f(x,y)在点(x0,y0)点处偏导数fx′(x0,y0)及fy′(x0,y0)存在,则f(x,y)在(x0,y0)处连续D以上说法都不对
单选题流行病学研究发现:某病暴露与两种不同的疾病X和Y有联系。对疾病X的相对危险度为6.0,特异危险度5%;对疾病Y的相对危险度为3.0,特异危险度为20%。据此,可以得出如下结论( )。A暴露与疾病X的联系强度是与疾病Y的联系强度的4倍B在未暴露者中,发生疾病Y的人数将足发生疾病X的人数的4倍C消除暴露后,减少的疾病Y的发病人数和减少的疾病X发病人数将不同D在暴露者中,发生疾病X的人数将是发生疾病Y的人数的1倍E以上都不是
单选题流行病学研究发现:某种暴露与两种不同的疾病X与Y有联系。对疾病X的相对危险度为6.0,特异危险度5%;对疾病Y的相对危险度为3.0,特异危险度为20%。根据上述资料,下列哪项说法是正确的?( )A在暴露者中,发生疾病X的人数将是发生疾病Y的人数的2倍B在未暴露者中,发生疾病Y的人数将是发生疾病X的人数的4倍C消除暴露后,减少的疾病Y的发病人数和减少的疾病X发病人数将不同D暴露与疾病X的联系强度是与疾病Y的联系强度的4倍E以上都不是
单选题流行病学研究发现:某种暴露与两种不同的疾病X与Y有联系。对疾病X的相对危险度为6.0,特异危险度5%;对疾病Y的相对危险度为3.0,特异危险度为20%。据此,可以得出如下结论( )。A暴露与疾病X的联系强度是与疾病Y的联系强度的4倍B在未暴露者中,发生疾病Y的人数将是发生疾病X的人数的4倍C消除暴露后,减少的疾病Y的发病人数和减少的疾病X发病人数将不同D在暴露者中,发生疾病X的人数将是发生疾病Y的人数的2倍E以上都不是