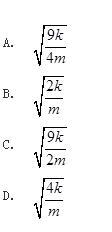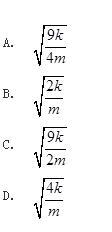由于结构的质量与刚度是结构固有的,因此无阻尼体系自振频率或周期也是体系固有的。()
如图所示,三根弹簧的刚性系数分别为k1,k2,k3,振体的质量为m,则此系统沿铅垂方向振动的固有圆频率为( )。
已知图示梁抗弯刚度EI为常数,则用叠加法可得跨中点C的挠度为:
图示弹簧一物块直线振动系统中,物块质量m,两根弹簧的刚度系数各为k1和k2。若用一根等效弹簧代替这两根弹簧,则其刚度系数k为:
在图示体系中,集中质量为m,杆长为l,抗弯刚度为EI,杆重不计。该体系自由振动的周期为( )。
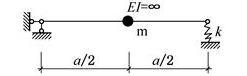
如图所示结构,集中质量m在刚性梁的中点,EI=∞,弹簧刚度为k,该体系自振频率为( )。
图示结构,质量m在杆件中点,EI=∞,弹簧刚度为k,该体系自振频率为( )。
图示三种体系的弹簧刚度均相同,则其自振频率的关系为:A.wa=wbB.wa=wcC.wb=wcD.都不相等
图示三种单自由度动力体系中,质量m均在杆件中点,各杆EI、l相同。其自振频率的大小排列次序为:A. a)>b)>c)B. c)>b)>a)C. b)>a)>c)D. a)>c)>b)
图示结构,EI为常数。结点B处弹性支撑刚度系数k=3EI/L3,C点的竖向位移为( )。
图示结构B处弹性支座的弹簧刚度k=12EI/l3,B截面的弯矩为( )。A. Pl/2B. Pl/3C. Pl/4D. Pl/6
图示结构,不计杆件分布质量,当EI2增大时,结构自振频率:A.不变B.增大C.减少D.不能确定
图示梁的抗弯刚度为EI,长度为l,欲使梁中点C弯矩为零,则弹性支座刚度k的取值应为( )
如图所示结构,刚性横梁质量为m,立柱无质量,刚度EI,其自振频率为( )。
结构自振频率与结构刚度具有相关性,实测自振频率大于计算值,说明结构刚度小于计算刚度。( )
图示结构连续梁的刚度为EI,梁的变形形式为( )。A.B.C.D.
在图示结构中,为使体系自振频率ω增大,可以()。 A增大PB增大mC增大EID增大
图示a、b两体系的EI相同,其自振频率ωa与ωb的关系为()。A不确定Bωa<ωbCωa=ωbDωa>ωb
求图示体系的自振频率。质量m集中在横梁上。各杆EI=常数。
某跨径为20m的预应力混凝土简支箱梁桥动力(自振)特性测定试验,诚完成以下相关试验设计、现场操作和分析等工作。以下相关分析正确的有()A、实测一、二阶竖向自振频率为5.50Hz和22.50Hz,可认为桥跨结构刚度大于计算刚度B、实测一阶竖向自振频率为5.5Hz,则桥跨结构刚度约为计算刚度的1.1倍C、实测一阶竖向自振频率为4.80Hz,可认为桥跨结构刚度大于计算刚度D、实测一阶竖向自振频率为15.01Hz,该数据严重异常,须重新进行试验