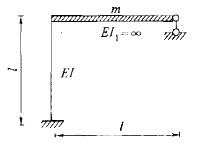
在图示体系中,集中质量为m,杆长为l,抗弯刚度为EI,杆重不计。该体系自由振动的周期为( )。
图示结构,质量m在杆件中点,EI=∞,弹簧刚度为k,该体系自振频率为( )。
设θ=0. 5w(w为自振频率),则图示体系的最大动位移为:
当图所示的体系反对称振动时,自振频率ω之值为( )。
如图中所示桁架体系,EA=C(这里C表示常数),则体系自振频率为( )。
图示梁自重不计,在集中重量W作用下,C点的竖向位移Δc =1cm,则该体系的自振周期为:A. 0.032sB. 0.201sC. 0. 319sD. 2. 007s
图示三种单自由度动力体系中,质量m均在杆件中点,各杆EI、l相同。其自振频率的大小排列次序为:A. a)>b)>c)B. c)>b)>a)C. b)>a)>c)D. a)>c)>b)
图a)体系的自振频率wa与图b)体系的自振频率wb的关系是:A. wabB. wa>wbC.wa=wbD.不能确定
图示结构,不计杆件分布质量,当EI2增大时,结构自振频率:A.不变B.增大C.减少D.不能确定
图示体系的自振频率为,其稳态最大动力弯矩幅值为:A. 3PlB. 4. 5PlC. 8. 54PlD. 2Pl
图示结构,集中质量m在刚性梁的中点,EI=∞,弹簧刚度为k,该体系自振频率为( )。
图示梁自重不计,在集中重量W作用下,C点的竖向位移Δc =1cm,则该体系的自振周期为:A. 0.032s B. 0.201s C. 0. 319s D. 2. 007s
在图示结构中,为使体系自振频率ω增大,可以()。 A增大PB增大mC增大EID增大
图示a、b两体系的EI相同,其自振频率ωa与ωb的关系为()。A不确定Bωa<ωbCωa=ωbDωa>ωb
求图示体系的自振频率。质量m集中在横梁上。各杆EI=常数。
图示结构中,使体系自振频率ω减小,可以()。 A减小FPB减小mC减小EID减小l
在图示结构中。使体系自振频率ω减小,可以()。 A增大PB减小mC减小EID减小l