如，正方体位于半径为3的球内，且其中一面位于球的大圆上，则正方体表面积最大为A.12B.18C.24D.30E.36

如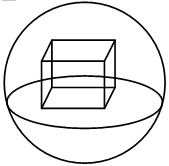，正方体位于半径为3的球内，且其中一面位于球的大圆上，则正方体表面积最大为

A.12
B.18
C.24
D.30
E.36

参考解析

解析：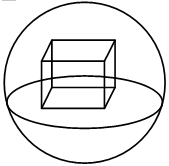

相关考题：

把一个64cm×40cm×24cm的长方体切成若干个完全相同的小正方体，并使这些小正方体的表面积总和最小，则小正方体的表面积总和为（ ）。A．73280cm2B．54680cm2C．69450cm2D．46080cm2
查看答案
把一个64Cmx40Cmx24Cm的长方体切成若干个完全相同的小正方体，并使这些小正方体的表面积总和最小，则小正方体的表面积总和为（ ）。A．73280cm2B．54680cm2C．69450cm2D．46080cm2
查看答案
把棱长为4的正方体分割成24个棱长为整数的正方体（且没有剩余），其中棱长为1的正方体的个数为（ ）A、 12B、 15C、 18D、 21
查看答案
在棱长为1的正方体上切下两个角，所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体，六面体体积为原正方体体积的1/24，则六面体表面积为原正方体表面积的：A.1/4B.1/6C.1/8D.1/10
查看答案
一个正方体的高增加10cm，得到新长方体的表面积比原正方体表面积增加120cm，原正方体体积是（　　）．A.9cm3B.12cm3C.18cm3D.27cm3
查看答案
将边长为1的正方体一刀切割为2个多面体，其表面积之和最大为： A.6+2√2B. 6+2√3C.6+√2D. 6+2√3
查看答案
将边长为1的正方体一刀切割为2个多面体，其表面积之和最大为：
查看答案
边长为6的正方体，由若干个边长为1的正方体组成，现将大正方体表面涂上色，请问仅有一面着色的小正方体与仅有两面着色的小正方体个数之差为多少？A.36B.48C.54D.64
查看答案
有一批边长为1厘米的小正方体，其中一面涂红色的有400个，相邻两面涂红色的有30个，相邻三面涂红色的有1个，其余小正方体各面都没有涂颜色。用这一批小正方体组成一个大正方体，要求这个大正方体有三个面是红色，且这三个面两两相邻，其余的三个面没有颜色。假如没有涂颜色的小正方体数量足够多，那么这个正方体的边长最大是（ ）厘米。A.10B.11C.12D.13
查看答案
已知球的大圆周长是π，则这个球的表面积是（　　）
查看答案
棱长等于1的正方体内接于一球体中，则该球的表面积是（　　）A.3πB.C.6πD.9π
查看答案
以下6个图形为正方体的外表面展开图，其中3个图形组成的正方体相同，另外3个图形组成的正方体也相同，问正确的分组是：A.①③⑤，②④⑥B.①③④，②⑤⑥C.①②⑤，③④⑥D.①③⑥，②④⑤
查看答案
把若干个体积相等的正方体拼成一个大正方体,在表面涂上红色,已知一面涂色的小正方体有96个,则两面涂色的小正方体有（ ）个A.48B.60C.64D.24E.32
查看答案
体积相等的球和正方体，它们的表面积的大小关系是（）。A、S球＞S正方体B、S球=S正方体C、S球＜S正方体D、不能确定
查看答案
热门标签