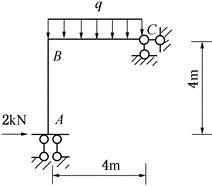
如图所示结构，EI为常数，欲使结点B的转角为零，则q的值为（　　）kN/m。 A、0 B、2 C、4 D、8

如图所示结构，EI为常数，欲使结点B的转角为零，则q的值为（　　）kN/m。


A、0
B、2
C、4
D、8

参考解析

解析：在结点B处附加刚臂，得到位移法基本体系，建立位移法基本方程得：k11Δ1+F1P=0，由于结点B的转角Δ1为零，所以

{图}

解得q=2kN/m。

相关考题：

图示结构EI=常数，截面A右侧的弯矩为()A.M/2B.MC.0D.M/(2EI)
查看答案
图示结构，EI＝常数，则结点B的角位移为（　　）。A．0B．ql3／（24EI）（顺时针）C．7ql3／（96EI）（顺时针）D．3ql3／（24EI）（顺时针）
查看答案
图所示的刚架，EI＝常数，各杆长为l，A截面的转角为（　　）。
查看答案
图示结构杆长为l，EI=常数，C点两侧截面相对转角φC为：
查看答案
已知刚架的弯矩图如图所示，杆的抗弯刚度为杆的为2EI，则结点B的角位移等于：
查看答案
图所示刚架，EI=常数，结点A的转角是（　　）。（提示：利用转动刚度的概念）
查看答案
图所示连续梁，EI为常数，用力矩分配法求得结点B的不平衡力矩为（　　）。 A、-20kN·m B、15kN·m C、-5kN·m D、5kN·m
查看答案
结构在荷载下的弯矩图如图所示，曲线为q＝2kN／m引起的二次抛物线，EI＝常数。B点的水平位移为（　　）。A．108／（EI）（→）B．756／（EI）（→）C．828／（EI）（→）D．900／（EI）（→）
查看答案
图示连续梁，EI=常数，已知支承B处梁截面转角为-7Pl2/240EI（逆时针向），则支承C处梁截面转角φC应为：
查看答案
如图所示的结构，EI＝常数，杆端弯矩（顺时针为正）正确的是（　　）。
查看答案
图示刚架EI=常数，结点B的水平位移为（　　）。
查看答案
图示刚架，EI为常数，结点A的转角是（　　）。（提示：利用对称性和转动刚度的概念）
查看答案
图示连续梁，EI=常数，欲使支承B处梁截面的转角为零，比值a/b应为：
查看答案
图所示结构EI为常数，用力矩分配法求得弯矩Mba是（　　）。 A、2kN·m B、-2kN·m C、8kN·m D、-8kN·m
查看答案
图示结构，EI=常数，欲使结点B的转角为零，比值P1/P2应为：A. 1. 5B. 2C. 2. 5D. 3
查看答案
如图所示的结构（EI＝常数）中，D点水平位移（向右为正）为（　　）。
查看答案
图示刚架，EI=常数，结点A的转角是（　　）。（提示：利用转动刚度的概念）
查看答案
如图所示组合结构，梁式杆件EI＝常数，桁架杆件EA＝常数，C点竖向位移为（　　）。 A、向上 B、向下 C、为零 D、需计算确定
查看答案
图所示刚架，EI为常数，结点A的转角是（　　）。（提示：利用对称性和转动刚度的概念）
查看答案
图示结构，EI为常数。结点B处弹性支撑刚度系数k=3EI/L3，C点的竖向位移为（　　）。
查看答案
图示连续梁，EI为常数，用力矩分配法求得结点B的不平衡力矩为（　　）。A、-20kN·mB、15kN·mC、-5kN·mD、5kN·m
查看答案
图示梁的抗弯刚度为EI，长度为l，欲使梁中点C弯矩为零，则弹性支座刚度k的取值应为（　　）
查看答案
图示连续梁，EI=常数，欲使支承B处梁截面的转角为零，比值a/b应为：A. 1/2B. 2C. 1/4D. 4
查看答案
图示为结构在荷载作用下的M图，各杆EI=常数，则支座B处截面的转角为:
查看答案
一无吊车工业厂房，采用刚性屋盖，跨度为15m，其铰接排架结构计算简图及所承受的荷载设计值如图所示。柱的截面尺寸为400mm×400mm，as＝40mm，混凝土强度等级为C30，结构安全等级为二级，纵向受力钢筋为HRB335。1.设P＝400kN，q＝30kN，柱的净高Hn＝6m，则排架左列柱柱底截面的内力设计值M、N、V最接近于（　　）。 A、M=90kN·m；N=400kN；V=15kN B、M=90kN·m；N=400kN；V=30kN C、M=100kN·m；N=800kN；V=15kN D、M=100kN·m；N=800kN；V=30kN
查看答案
计算图示刚架结点C的水平位移和转角，EI=常数。
查看答案
单选题图示结构，EI=常数，欲使结点B的转角为零，比值P1/P2应为：（）A 1.5B 2C 2.5D 3
查看答案
热门标签