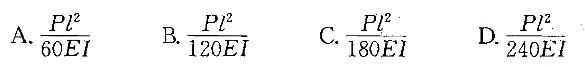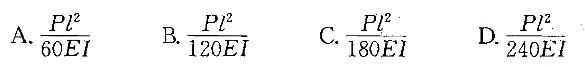根据梁的变形与弯矩的关系,在下列说法中正确的是() A、正弯矩产生正转角,负弯矩产生副转角B、弯矩最大的截面转角最大,弯矩为零的截面上转角为零C、弯矩为零处,挠曲线曲率必为零D、梁的最大挠度必发生在弯矩最大处
连续梁由于中间支承处梁的弯曲力矩较大,所以往往在该处梁身做成折线形或曲线形以增加截面高度来进行加强。() 此题为判断题(对,错)。
梁的挠度和转角除了与梁的支承和荷载情况有关外,还取决于()。A、材料B、截面C、跨长D、周围环境
图示为梁在实际状态下的MP图,EI=常数,则K截面的角位移46.6/EI。()此题为判断题(对,错)。
图示梁AB,EI为常数,固支端A发生顺时针的支座转动θ,由此引起的B端转角为:A.θ,顺时针B.θ,逆时针C.θ/2,顺时针D.θ/2,逆时针
图示结构,当支座B发生沉降Δ时,支座B处梁截面的转角大小为:
图示结构EI=常数,当支座A发生转角θ支座B处截面的转角为(以顺时针为正)( )。A.θ/3B.2θ/5C.-θ/3D.-2θ/5
图示梁AB,EI为常数,固支端A发生顺时针的支座转动,由此引起的B处的转角为( )。
图示连续梁,EI=常数,欲使支承B处梁截面的转角为零,比值a/b应为:
图示刚架EI=常数,截面C和D的相对转角为( )。
图所示梁AB,EI为常数,固支端A发生顺时针的支座转动θ,由此引起的B处的转角为( )。{图} A.θ,顺时针 B.θ,逆时针 C.θ/ 2,顺时针 D.θ/ 2,逆时针
图示梁铰C左侧截面的转角时,其虚拟单位力状态应取:
图示连续梁,EI=常数,欲使支承B处梁截面的转角为零,比值a/b应为:A. 1/2B. 2C. 1/4D. 4
图示结构EI=常数,当支座B发生沉降Δ时,支座B处梁截面的转角为(以顺时针为正)( )。A、Δ/lB、1、2Δ/lC、1、5Δ/lD、Δ/2l
求图示梁铰C左侧截面的转角时,其虚拟单位力状态应取:
图示为结构在荷载作用下的M图,各杆EI=常数,则支座B处截面的转角为:
连续梁由于中间支承处梁的弯曲()较大,所以在该处梁身做成折线形或曲线形以增加截面高度来进行加强。A、力矩B、活载C、静载D、荷载
有一简支梁,中点受集中力P作用。梁端转角θ=Pl2/16EI,当梁的长度l、横截面尺寸、荷载P均增大一倍时,梁端转角等于原转角的多少倍?()A、1/2B、1C、2D、4
梁弯曲时,某截面处挠曲线的切线相对于变形前梁轴线的倾角,称为转角。
单选题连续梁由于中间支承处梁的弯曲()较大,所以在该处梁身做成折线形或曲线形以增加截面高度来进行加强。A力矩B活载C静载D荷载
单选题图示结构El=常数,当支座B发生沉降△时,支座B处梁截面的转角为(以顺时针为正)( )。A △/lB 1.2△/lC 1.5△/lD △/2l