某超市欲从深圳某公司购进一批净水器,为了检验该产品的质量,超市随机抽取25件净水器进行使用寿命的测试,产品的使用寿命服从正态分布,测得结果如下,平均使用寿命为1061小时,标准差为66.96小时。该超市要求以95%的置信水平估计该批净水器使用寿命的置信区间。
某超市欲从深圳某公司购进一批净水器,为了检验该产品的质量,超市随机抽取25件净水器进行使用寿命的测试,产品的使用寿命服从正态分布,测得结果如下,平均使用寿命为1061小时,标准差为66.96小时。该超市要求以95%的置信水平估计该批净水器使用寿命的置信区间。
参考解析
解析: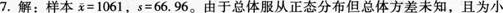

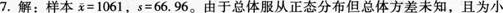

相关考题:
设某产品使用寿命X服从正态分布,要求平均寿命不低于1000小时,现从一批这种产品中随机抽出25只,测得平均寿命为950小时,方差为100小时,检验这批产品是否合格可用()。 A、t检验法B、χ2检验法C、Z检验法D、F检验法
下列随机事件中,随机变量为离散型随机变量的有( )。A.一顾客在超市等候付款的时间B.一天内进入某超市的顾客数C.一批产品中合格品的个数D.某公司客服中心一天接到的电话数E.某台机床的使用寿命
某企业生产的袋装食品采用自动打包机包装,每袋标准重量为100克。现从某天生产的一批产品中按重复抽样随机抽取50包进行检查,测得样本均值为:(1)确定该种食品平均重量95%的置信区间。(2)采用假设检验方法检验该批食品的重量是否符合标准要求?(写出检验的具体步骤)。
某超市欲从深圳某公司购进一批净水器,为了检验该产品的质量,超市随机抽取25件净水器进行使用寿命的测试,产品的使用寿命服从正态分布,测得结果如下,平均使用寿命为1061小时,标准差为66.96小时。该超市要求以95%的置信水平估计该批净水器使用寿命的置信区间。
为了考察某种类型的电子元件的使用寿命情况,假定该电子元件使用寿命的分布是正态分布。而且根据历史记录得知该分布的参数为:平均使用寿命μ0为100小时,标准差口为10小时。现在随机抽取100个该类型的电子元件,测得平均寿命为102小时,给定显著性水平α=0.05,为了判断该电子元件的使用寿命是否有明显的提高,下列说法正确的有( )。A.提出假设H0:μ≤100;H1:μ>100B.提出假设H0:μ≥100;H1:μ<100C.检验统计量及所服从的概率分布为D.如果Z>Zα,则称与μ0的差异是显著的,这时拒绝H0E.检验结果认为该类型的电子元件的使用寿命确实有显著提高
下列随机事件中,随机变量为离散型随机变量的有( )。A. 一顾客在超市等候付款的时间 B. —天内进入某超市的顾客数C. 一批产品中合格品的个数 D.某公司客服中心一天接到的电话数E.某台机床的使用寿命
某种元件使用寿命X~N(μ,10^2).按照客户要求该元件使用寿命不能低于1000h,现从该批产品中随机抽取25件,其平均使用寿命为x=995,在显著性水平α=0.05下确定该批产品是否合格?
关于抽样检验,下列说法正确的是()。A:从一批产品中随机抽取的一部分进行试验,通常检验少量的该产品来对产品的质量进行评估的方法,决定质量是否合格的结论B:从一批产品中随机抽取的一部分进行试验,通常检验大量的该产品来对产品的质量进行评估的方法,决定质量是否合格的结论C:从一批产品中有目的抽取的一部分进行试验,通常检验少量的该产品来对产品的质量进行评估的方法,决定质量是否合格的结论D:从一批产品中随机抽取的一部分进行试验,通常检验少量的该产品来对产品的质量进行预测的方法
(二)质检人员从生产线上随机抽取5件产品检验其使用寿命,产品的质量标准是使用寿命不小于100小时。5件产品的使用寿命(单位:小时)分别为125、100、115、90、125。请根据上述资料回答下列问题:已知产品的使用寿命服从正态分布,样本方差为S2,样本均值为 ,则生产线上该种产品平均使用寿命95%的置信区间为( )。(注:Z0.025=1.96,t0.025(4)=2.776)
(二)质检人员从生产线上随机抽取5件产品检验其使用寿命,产品的质量标准是使用寿命不小于100小时。5件产品的使用寿命(单位:小时)分别为125、100、115、90、125。请根据上述资料回答下列问题:5件产品使用寿命的( )。
(二)质检人员从生产线上随机抽取5件产品检验其使用寿命,产品的质量标准是使用寿命不小于100小时。5件产品的使用寿命(单位:小时)分别为125、100、115、90、125。请根据上述资料回答下列问题:根据产品质量标准和抽样调查结果,可得样本的合格率p为( )。A.60%B.70%C.80%D.90%
为了考察某种类型的电子元件的使用寿命情况,假定该电子元件使用寿命的分布是正态分布。而且根据历史记录得知该分布的参数为:平均使用寿命μ0为100小时,标准差a为10小时。现在随机抽取100个该类型的电子元件,测得平均寿命为102小时,给定显著性水平a=0.05,为了判断该电子元件的使用寿命是否有明显的提高,下列说法正确的有( )。
(二)某种产品的质量标准是直径为23厘米。为检验自动生产线是否正常,质检人员从生产线上随机抽取10件产品进行检测,测得产品的直径数据(单位:厘米)分别为23、18、22、21、27、25、19、21、24、17。如果产品的直径服从正态分布, ,样本方差为 ,样本均值为 ,则生产线上该种产品平均直径95%的置信区间为( )。
某超市果蔬汁平均日需求量为200瓶,需求情况服从标准差为10瓶/天的正态分布。如果提前期是固定常数4天,客户服务水平为95%,对应的安全系数为1.65,那么该超市果蔬汁的安全库存量应为()瓶。A:33B:44C:55D:66
某企业生产一批零件,随机重复抽取400只做使用寿命试验。测试结果平均寿命为5000小时,样本标准差为300小时,400只中发现10只不合格。根据以上资料计算平均数的抽样平均误差和成数的抽样平均误差。
某一种净水器经过对其出水水质的检验显示浊度为0.5,细菌总数为10CFU/ml,溶解性总固体600ml/L,色度3度,砷0.01mg/L,据此认为该水质()A、符合净水器水质卫生要求B、浊度不符合净水器水质卫生要求C、细菌总数不符合净水器水质卫生要求D、溶解性总固体不符合净水器水质卫生要求E、色度不符合净水器质水质卫生要求
某电子元件厂某月生产电子管10000个,采用随机抽样检验产品的平均使用寿命和产品合格率,样本容量为180个,检验结果180个电子管的平均使用寿命为3880小时,产品合格数为174个。要求推断该批电子管的平均使用寿命、产品合格率和总合格品数。
问答题某工厂收到供货方发来的一批电子元件的例子中,共抽取了10件电子元件进行检验,使用样本的方差为S2=8000.56(小时)。试在95%的置信概率下对该批电子元件使用寿命的方差和标准差进行区别。
单选题某超市“HY果汁”平均日需求量为100箱,且需求情况服从标准差为10箱/天的正态分布,如果提前期是固定常数4天,客服服务水平不低于95%(95%对应安全系数为1.65),那么该超市“HY果汁”的安全库存为( )箱。A23B33C38D50
多选题(二)质检人员从生产线上随机抽取5件产品检验其使用寿命,产品的质量标准是使用寿命不小于100小时。5件产品的使用寿命(单位:小时)分别为125、100、115、90、125。请根据上述资料回答下列问题:5件产品的使用寿命( )。A中位数为115B算术平均数为111C呈左偏态分布D呈右偏态分布
问答题某超市想要估计每个顾客平均每次购物花费的金额。根据过去的经验,标准差大约为 120元,现要以95%的置信水平估计每个顾客平均每次购物金额的置信区间,并要求边际误差不超过20元,若采用不重复抽样,要抽取多少个顾客作为样本?