如图所示的连续梁，已知F、l、φB、φC，则可得出（　　）。

如图所示的连续梁，已知F、l、φB、φC，则可得出（　　）。



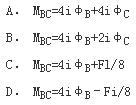
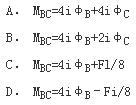
参考解析

解析：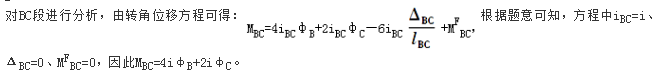

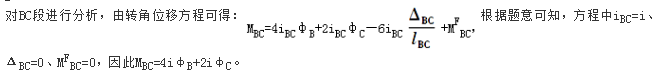
相关考题：

已知（F/P,3%,6）＝1.1941，则可以计算出（P/A,3%,6）＝3.47。（ ）
查看答案
如图所示矩形截面梁,已知材料的许用正应力[σ]=170MPa,许用切应力[τ]=100MPa。试校核梁的强度。
查看答案
平面钢架受力如图所示，已知F=50kN，忽略钢架自重，求钢架A、D处的支座反力。
查看答案
如图所示单跨静定梁的计算简图，已知F1=30kN，F2=40kN，L=10m，a=4m，b=6m，c=2m。支座反力RAy为()kN。A.30B.34C.35D.36
查看答案
一矩形截面简支梁，梁上荷载如图所示。已知P=6kN、l=4m、b=0.1m、h=0.2m，画出梁的剪力图和弯矩图并求梁中的最大正应力。
查看答案
图所示为一连续梁，已知q、a及θ，不计梁的自重，求A、B、C三处的约束力。
查看答案
梁结构尺寸、受力如图所示，不计梁重，已知q=10kN/m，M=10kN·m，求A、B、C处的约束力。
查看答案
已知简支梁受如图所示荷载，则跨中点C截面上的弯矩为：
查看答案
—铸铁梁如图所示，已知抗拉的许用应力[σt]c]，则该梁截面的摆放方式应如何图所示？
查看答案
如图所示电路中，已知： A． 7.39μF和71.14μF B． 71.14μF和7.39μF C． 9.39μF和75.14μF D． 75.14μF和9.39μF
查看答案
已知曲线，其中函数f(t)具有连续导数，且f(0)=0，f'(t)>0(0).若曲线L的切线与x轴的交点到切点的距离恒为1，求函数f(t)的表达式，并求以曲线L及x轴和y轴为边界的区域的面积.
查看答案
如图所示，两跨连续梁的中间支座B及右端支座C分别产生竖向沉陷2Δ及Δ，由此引起的截面A的弯矩MAB之值为（　　）。
查看答案
如图所示，已知梁高h＝500mm，跨度l＝4m，梁支承长度240mm，墙体厚度h′＝240mm，砌体抗压强度设计值f＝1.5MPa，则屋面梁下墙顶截面的偏心距e值为（　　）mm。 A、47 B、61 C、120 D、178
查看答案
图示连续梁，EI=常数，已知支承B处梁截面转角为-7Pl2/240EI（逆时针向），则支承C处梁截面转角φC应为：
查看答案
如图所示的简支梁，当单位荷载F＝1在其AC段上移动时，弯矩Mc的影响线方程为（　　）。 A、－（l－x）a/l B、－x·b/l C、（l－x）a/l D、x·b/l
查看答案
一简支梁截面惯性矩为7480cm3，抗弯截面模量为534.286cm3。跨中承受一集中荷载如图所示。已知：F=20kN,l=9m,E=210GPa,[σ]=90MPa,试校核梁的正应力强度（ ）。A.82.13MPa＜[σ]=90MPaB.,95.2MPa>[σ]=90MPaC.84.27MPa＜[σ]=90MPaD.93.1MPa>[σ]=90MPa
查看答案
已知条件如图所示，力F1在工坐标轴上的投影为（ ）。A.1/2F1B.根号2/2F1C.F1D.根号3/2F1
查看答案
悬臂梁的弯矩如图所示，根据梁的弯矩图，梁上的载荷F、m的值应是:A. F=6kN,m=10kN * mB. F=6kN，m=6kN * mC. F=4kN,m=4kN * mD. F=4kN，m=6kN * m
查看答案
已知椭圆C的中心在原点，焦点F1.F2在x轴上且经过点(1)求椭圆C的方程； (2)如图所示，若直线Z经过椭圆C的右焦点F2且与椭圆C交于A，B两点，使得求直线l的方程。
查看答案
已知函数f(x)在闭区间[a,b].上连续，且f(a).f(b)
查看答案
已知,那么（ ）。A. f(x)在x = 0处不连续 B. f(x)在x=0处连续
查看答案
已知如图所示的一个图，若从顶点a出发，按深度优先搜索法进行遍历，则可能得到的一种顶点序列为（）。 AabecdfBacfebdCaedfcbDaebcfd
查看答案
圆截面简支梁如图所示，已知F=1KN，回答下列问题。 若梁直径d=40mm，求梁的最大应力。
查看答案
求图所示梁支座的约束反力。已知F=2KN。
查看答案
单选题如图所示，伸臂梁F=qa/2，M=2qa2，已知q、a，则B点的约束反力是()。[img:LzIwMTctMDMveWVuaS8yMDE3MDMzMTE1MTEyMTU4MjQ4LnBuZw==]AqaBqa/2C3qa/2D2qa
查看答案
判断题已知（F/P，3%，6）＝1.1941，则可以计算出（P/A，3%，6）＝3.47。（）A对B错
查看答案
单选题如图所示，伸臂梁F=qa/2，M=2qa2，已知q、a，则B点的约束反力是()。[img:LzIwMTctMDQvemhhbmd5YW9yb25nLzIwMTcwNDA2MDkyMTQwOTQ2OTMucG5n]AqaBqa/2C3qa/2D2qa
查看答案
热门标签