如图所示的简支梁,当单位荷载F=1在其AC段上移动时,弯矩Mc的影响线方程为( )。 A、-(l-x)a/l B、-x·b/l C、(l-x)a/l D、x·b/l
如图所示的简支梁,当单位荷载F=1在其AC段上移动时,弯矩Mc的影响线方程为( )。
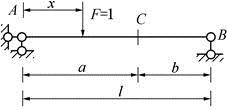

A、-(l-x)a/l
B、-x·b/l
C、(l-x)a/l
D、x·b/l
B、-x·b/l
C、(l-x)a/l
D、x·b/l
参考解析
解析:当单位荷载F=1作用在距A端x位置时,支座B的支反力

则由截面法可得,弯矩MC的影响线方程为
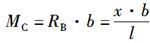

则由截面法可得,弯矩MC的影响线方程为
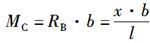
相关考题:
有关简支梁的受力特性,下列说法中正确的有( )。A.梁上、下边缘压拉应力大小与截面处弯矩Mc成正比B.截面弯矩Mc越大,梁上下边缘压、拉应力也越大C.均布荷载作用下的简支梁,跨中处弯矩最大D.均布荷载作用下的简支梁,支座处剪力最大E.均布荷载作用下的简支梁,跨中处弯矩和剪力最大
图(b)所示的是梁的某截面C的弯矩MC的影响线,单位为m。在图(a)所示移动荷载作用下,MC的最大值为( )。A、48、0kN·mB、53、6kN·mC、56、8kN·mD、57、4kN·m
有关简支梁的受力特性,下列说法中正确的有()。A:梁上、下边缘压拉应力大小与截面处弯矩Mc成正比B:截面弯矩Mc越大,梁上下边缘压、拉应力也越大C:均布荷载作用下的简支梁,跨中处弯矩最小D:均布荷载作用下的简支梁,支座处剪力最大
关于如图所示受力的简支梁在截面C处的剪力Q和弯矩M,描述正确的是( )。A.QC(左)=QC(右),MC(左)=MC(右)B.QC(右)=QC(左)+F,MC(左)=MC(右)C.QC(右)=QC(左)-F,MC(左)=MC(右)D.QC(右)=QC(左)-F,MC(左)≠MC(右)
单选题关于连续梁桥与简支梁桥的受力特点,下列说法正确的是( )。A连续梁支座位置弯矩为正弯矩B简支梁跨中弯矩为负弯矩C连续梁支座位置弯矩均为零D简支梁支座位置弯矩均为零