一绳索跨过匀质滑轮B,绳的一端挂一重物A;另一端缠绕一匀质圆柱C,如图所示。已知重物A的质量为mA;定滑轮B和圆柱C的质量分别为mB和mC,它们的半径均为r。绳的质量略去不计,它对定滑轮无相对滑动。设mB=mC=2mA,则定滑轮与圆柱之间绳索的拉力T为( )。
一绳索跨过匀质滑轮B,绳的一端挂一重物A;另一端缠绕一匀质圆柱C,如图所示。已知重物A的质量为mA;定滑轮B和圆柱C的质量分别为mB和mC,它们的半径均为r。绳的质量略去不计,它对定滑轮无相对滑动。设mB=mC=2mA,则定滑轮与圆柱之间绳索的拉力T为( )。
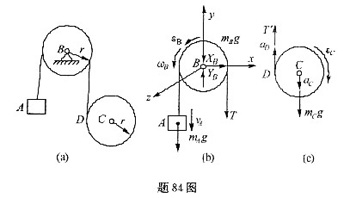



参考解析
解析:以定滑轮B连同重物A为研究对象,根据动量定理和刚体平面运动微分方程求解
相关考题:
在重力大小为W、半径为r的卷筒A上,作用一力偶矩m =aφ的力偶,其中φ为转角,a为常数。卷筒的绳索拉动水平面上的重物B(如图所示)。设重物B的重力大小为WB,它与水平面之间的动滑动摩擦系数为f',绳的质量不计。当卷筒转过两圈时,作用于系统上的力偶的功W1和摩擦力的功W2分别为:
一绳索跨过匀质滑轮B,绳的一端挂一重物A;另一端缠绕一匀质圆柱C,如图所示。已知重物A的质量为mA;定滑轮B和圆柱C的质量分别为mB和mC,它们的半径均为r。绳的质量略去不计,它对定滑轮无相对滑动。设mB=mC=2mA,则定滑轮与圆柱之间绳索的拉力T为( )。
质量为m,半径为r 的定滑轮O 上绕有细绳。依靠摩擦使绳在轮上不打滑,并带动滑轮转动。绳之两端均系质量m 的物块A 与B。块B放置的光滑斜面倾角为α ,假定定滑轮O 的轴承光滑,当系统在两物块的重力作用下开始运动时,B与O间,A 与O间的绳力FT1和FT2的大小有关系:(A) FT1=FT2(B) FT1 T2(C) FT1 >FT2(D)只根据已知条件不能确定
如图5所示,用跨过光滑定滑轮的绳将水平面上没有动力的小船沿直线拖向岸边。若拖动绳的电动机功率恒为P,小船质量为m,小船受到的阻力大小恒为f,经过A点时,绳与水平方向夹角为θ,小船速度大小为V0。,绳的质量忽略不计,则此时小船加速度α和绳对船的拉力F的大小为()。
长度为L的轻绳固定在水平天花板A点和竖直墙B点,绳上挂一定滑轮(质量不计),滑轮下吊一重物C,两绳之间夹角为θ,当绳子缓慢从B点移到动B’点后,则以下说法正确的是()A、绳的拉力不变B、绳的拉力变小C、θ角变大D、θ角减小
线度相同的滑块和匀质圆柱体,从同一固定斜面顶端由静止出发分别沿斜面向下滑动和纯滚动、不计空气阻力,若它们质量相同,则到达斜面底部时的动能()A、滑块较大B、圆柱体的较大C、一样大D、条件不足无法确定
体重相同的两人,同时沿均质定滑轮两侧的绳索由静止开始爬绳,绳子与人之间以及绳子与滑轮之间都无相对滑动,不计轴O摩擦,设整个系统的动量为p,对轴O的动量矩为LO,则()。A、p、LO守恒B、p守恒,LO不守恒C、LO守恒,p不守恒D、p、LO都不守恒
圆柱体定滑轮的质量为m,半径为R,绕其质心轴转动的角位移为θ=a+bt+ct2,a、b、c为常数,作用在定滑轮上的力矩为()A、(1/2)maR2B、bmR2C、(1/2)mbR2D、mcR2
单选题静止状态下,定滑轮绳索一端的拉力与被吊重物的重力是()的。A相等B拉力大于重力C重力大于拉力D两倍关系