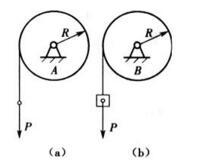
在两个半径及质量均相同的均质滑轮A及B上,各绕一不计质量的绳,如图所示,轮B绳末端挂一重量为P的重物;轮A绳末端作用一铅垂向下的力P。则此两轮的角加速度大小之间的关系为( )。
在两个半径及质量均相同的均质滑轮A及B上,各绕一不计质量的绳,如图所示,轮B绳末端挂一重量为P的重物;轮A绳末端作用一铅垂向下的力P。则此两轮的角加速度大小之间的关系为( )。


参考解析
解析:

相关考题:
质量m1与半径r均相同的三个均质滑轮,在绳端作用有力或挂有重物,如图所示。已知均质滑轮的质量为m1=2kN·s^2/m,重物的质量分别为m2=2kN·s^2/m,m3=1kN·s^2/m,重力加速度按g=10m/s^2计算,则各轮转动的角加速度α间的关系是( )。 A. α1=α3>α2 B. α1<α2<α3 C. α1>α3>α2 D. α1≠α2=α3
一绳索跨过匀质滑轮B,绳的一端挂一重物A;另一端缠绕一匀质圆柱C,如图所示。已知重物A的质量为mA;定滑轮B和圆柱C的质量分别为mB和mC,它们的半径均为r。绳的质量略去不计,它对定滑轮无相对滑动。设mB=mC=2mA,则定滑轮与圆柱之间绳索的拉力T为( )。
图示两重物的质量均为m,分别系在两软绳上。此两绳又分别绕在半径各为r与2r,并固结在一起的两圆轮上。两圆轮构成的鼓轮的质量亦为m,对轴O的回转半径为ρ0外。两重物中一铅垂悬挂,一置于光滑平面上。当系统在左重物重力作用下运动时,鼓轮的角加速度α为:
两重物的质量均为m,分别系在两软绳上。此两绳又分别绕在半径各为r与2r并固结在一起的两轮上。两圆轮构成之鼓轮的质量亦为m,对轴O的回转半径为ρO。两重物中一铅垂悬挂,一置于光滑平面上。当系统在左重物重力作用下运动时,鼓轮的角加速度α为:
两重物的质量均为m,分别系在两软绳上,此两绳又分别绕在半径各为r与2r并固结一起的两圆轮上,两圆轮构成之鼓轮的质量亦为m,对轴O的回转半径为p0,两重物中一铅垂悬挂,一置于光滑平面上,当系统在左重物重力作用下运动时,鼓轮的角加速度a为:
均质细杆AB重力为P,长为2l,A端铰支,B端用绳系住,处于水平位置,如图所示。当B端绳突然剪断瞬时,AB杆的角加速度大小为3g/4l,则A处约束力大小为:A. FAx= 0,FAy=0 B. FAx= 0,FAy=P/4 C. FAx= P,FAy=P/2 D.FAx= 0,FAy=P
一轻绳吊在有水平轴的定滑轮上,滑轮的转动惯量为J,绳下端挂一物体,物体所受重力为P,滑轮的角加速度为β。若将物体去掉而以P相等的力直接向下拉绳子,滑轮的角加速度β将( )。《》( )A.变大B.变小C.不变D.无法判断
一轻绳绕在有水平轴的定滑轮上,滑轮的转动惯量为J,绳下端挂一物体。物体所受重力为P,滑轮的角加速度为α。料将物体去掉而以与P相等的力直接向下拉绳子,滑轮的角加速度将( )。《》( )A.不变B.变小C.变大D.如何变化无法判断
长度为L的轻绳固定在水平天花板A点和竖直墙B点,绳上挂一定滑轮(质量不计),滑轮下吊一重物C,两绳之间夹角为θ,当绳子缓慢从B点移到动B’点后,则以下说法正确的是()A、绳的拉力不变B、绳的拉力变小C、θ角变大D、θ角减小
使用一动滑轮将一物体匀速提起的过程中,不计滑轮与绳的质量及其间的摩擦力,则()A、绳中的拉力一定等于被提物体的重量B、绳中的拉力一定等于被提物体重量的一半C、绳中的拉力可能大于被提物体的重量D、绳中的拉力可能小于被提物体的重量
半径为R具有光滑轴的定滑轮边缘绕一细绳,绳的下端挂一质量为m的物体绳的质量可以忽略,绳与定滑轮之间无相对滑动若物体下落的加速度为a,则定滑轮对轴的转动惯量J=()。