与n阶单位矩阵E相似的矩阵是A.B.对角矩阵D(主对角元素不为1)C.单位矩阵ED.任意n阶矩阵A
与n阶单位矩阵E相似的矩阵是
A.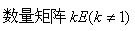
B.对角矩阵D(主对角元素不为1)
C.单位矩阵E
D.任意n阶矩阵A
A.
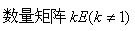
B.对角矩阵D(主对角元素不为1)
C.单位矩阵E
D.任意n阶矩阵A
参考解析
解析:
相关考题:
设A为m×n矩阵,B为n×m矩阵,E为m阶单位矩阵,若AB=E,则 A.A秩r(A)=m,秩r(B)=mB.秩r(A)=m,秩r(B)=nC.秩r(A)=n,秩r(B)=mD.秩r(A)=n,秩r(B)=n
设A为m×n矩阵,B为n×m矩阵,E为m阶单位矩阵,若AB=E,则( ).《》( )A.r(A)=m,r(B)=mB.r(A)=m,r(B)=nC.r(A)=n,r(B)=mD.r(A)=n,r(B)=n
单选题设A为m×n矩阵,B为n×m矩阵,E为m阶单位矩阵,若AB=E,则( )。Ar(A)=m,r(B)=mBr(A)=m,r(B)=nCr(A)=n,r(B)=mDr(A)=n,r(B)=n
问答题设A=E-α(→)α(→)T,其中E是n阶单位矩阵,α(→)是n维非零列向量,α(→)T是α(→)的转置。证明: (1)A2=A的充要条件是α(→)Tα(→)=1; (2)当α(→)Tα(→)=1时,A是不可逆矩阵。
单选题设n维向量α(→)=(a,0,…,0,a)T,a<0,E为n阶单位矩阵,矩阵A=E-α(→)α(→)T,B=E+α(→)α(→)T/a,且B为A的逆矩阵,则a=( )。A4B2C-1D1
单选题设A为n阶方阵,E为n阶单位矩阵,且A2=A,则(A-2E)-1=( )。AA+2EBA+EC(A+E)/2D-(A+E)/2