初中数学《勾股定理的逆定理》一、考题回顾
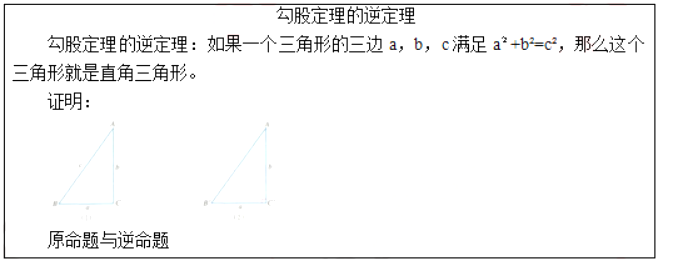
初中数学《勾股定理的逆定理》
一、考题回顾

一、考题回顾

参考解析
解析:二、考题解析
【教学过程】
(一)引入新课
引导学生复习勾股定理,并向学生提问:怎么画一个直角三角形?
预设:用三角尺。
提问:如果不用三角尺,怎么画直角三角形?并给学生出示古埃及人画直角三角形的情景,并引导学生思考:其中蕴含着什么规律呢?进而引出课题。
(二)探索新知
对于导入中的问题,教师可先引导学生思考3,4,5有什么样的关系?预设:32+42=52。
再继续出示几组数据:2.5,6,6.5以及4,7.5,8.5引导学生采用尺规作图。并观察做出的三角形的形状。
引导学生大胆猜想,得到:如果三角形的三边长分别为a,b,c,满足a2+b2=c2,那这个三角形就是一个直角三角形。
提问:那怎么证明这个猜想是正确的?
引导学生采用尺规作图的方式,做出和已知三角形三边相同的直角三角形,利用勾股定理得出三角形的对应的三边相等,进而两个三角形全等,也就证明上述的猜想是正确的。
引导学生观察勾股定理和命题2,说说两个命题有什么样的关系?
预设:两个命题的条件和结论是相反。
进而给出原逆命题的概念。并给说明上述的发现也是一个定理,称为勾股定理的逆定理。
提问:原命题正确,逆命题一定正确?
预设:对顶角相等,但是两个角相等,不一定是对顶角。
最后,师生共同得出:原命题正确,逆命题不一定正确,只有正确的逆命题才能叫做原命题的逆定理。
(三)课堂练习
判断由线段a,b,c组成的三角形是不是直角三角形。
(1)a=15,b=8,c=17;(2)a=13,b=14,c=15。
(四)小结作业
提问:今天有什么收获?
课后作业:课后作业1-3。
【板书设计】
【答辩题目解析】
1.谈一谈勾股定理在初中教材中的地位?
【参考答案】
勾股定理是初中几何中几个重要定理之一。它揭示了直角三角形三边的某种数量关系。勾股定理是建立在三角形、全等三角形、等腰三角形等有关知识的基础之上,同时也是初三几何中解直角三角形及圆中有关计算的必备知识。更重要的是,纵观整个初中数学,勾股定理架起了代数与几何之间的桥梁。勾股定理在数学理论体系中的地位举足轻重,在日常生活、工农业生产中,应用极为广泛。就学生而言,对勾股定理学习的好坏将直接影响到他们后续数学的学习。
2.教学过程中你主要设置了哪些问题,目的是什么?
【参考答案】
第一个问题:把一根长绳打上13个绳结,以3、4、5个结间距为边长组成的三角形中就有一个是直角。用这样的绳结组成的三角形是直角三角形么?
设计意图:通过这样的古代数学问题激发学生的学习兴趣,从而引出本节课的课题《勾股定理的逆定理》。
第二个问题:动手操作导入问题以及2.5,6,6.5;6,8,10能否组成直角三角形?根据以上结论能得出什么猜想?
设计意图:鼓励学生动手探究提升综合实践能力,进一步根据事实作出猜想提升合情推理能力。
第三个问题:这个命题正确么?
设计意图:鼓励学生对猜想进行证明养成良好的反思质疑的学习习惯并进一步提升演绎推理能力。
【教学过程】
(一)引入新课
引导学生复习勾股定理,并向学生提问:怎么画一个直角三角形?
预设:用三角尺。
提问:如果不用三角尺,怎么画直角三角形?并给学生出示古埃及人画直角三角形的情景,并引导学生思考:其中蕴含着什么规律呢?进而引出课题。
(二)探索新知
对于导入中的问题,教师可先引导学生思考3,4,5有什么样的关系?预设:32+42=52。
再继续出示几组数据:2.5,6,6.5以及4,7.5,8.5引导学生采用尺规作图。并观察做出的三角形的形状。
引导学生大胆猜想,得到:如果三角形的三边长分别为a,b,c,满足a2+b2=c2,那这个三角形就是一个直角三角形。
提问:那怎么证明这个猜想是正确的?
引导学生采用尺规作图的方式,做出和已知三角形三边相同的直角三角形,利用勾股定理得出三角形的对应的三边相等,进而两个三角形全等,也就证明上述的猜想是正确的。
引导学生观察勾股定理和命题2,说说两个命题有什么样的关系?
预设:两个命题的条件和结论是相反。
进而给出原逆命题的概念。并给说明上述的发现也是一个定理,称为勾股定理的逆定理。
提问:原命题正确,逆命题一定正确?
预设:对顶角相等,但是两个角相等,不一定是对顶角。
最后,师生共同得出:原命题正确,逆命题不一定正确,只有正确的逆命题才能叫做原命题的逆定理。
(三)课堂练习
判断由线段a,b,c组成的三角形是不是直角三角形。
(1)a=15,b=8,c=17;(2)a=13,b=14,c=15。
(四)小结作业
提问:今天有什么收获?
课后作业:课后作业1-3。
【板书设计】

【答辩题目解析】
1.谈一谈勾股定理在初中教材中的地位?
【参考答案】
勾股定理是初中几何中几个重要定理之一。它揭示了直角三角形三边的某种数量关系。勾股定理是建立在三角形、全等三角形、等腰三角形等有关知识的基础之上,同时也是初三几何中解直角三角形及圆中有关计算的必备知识。更重要的是,纵观整个初中数学,勾股定理架起了代数与几何之间的桥梁。勾股定理在数学理论体系中的地位举足轻重,在日常生活、工农业生产中,应用极为广泛。就学生而言,对勾股定理学习的好坏将直接影响到他们后续数学的学习。
2.教学过程中你主要设置了哪些问题,目的是什么?
【参考答案】
第一个问题:把一根长绳打上13个绳结,以3、4、5个结间距为边长组成的三角形中就有一个是直角。用这样的绳结组成的三角形是直角三角形么?
设计意图:通过这样的古代数学问题激发学生的学习兴趣,从而引出本节课的课题《勾股定理的逆定理》。
第二个问题:动手操作导入问题以及2.5,6,6.5;6,8,10能否组成直角三角形?根据以上结论能得出什么猜想?
设计意图:鼓励学生动手探究提升综合实践能力,进一步根据事实作出猜想提升合情推理能力。
第三个问题:这个命题正确么?
设计意图:鼓励学生对猜想进行证明养成良好的反思质疑的学习习惯并进一步提升演绎推理能力。
相关考题:
《勾股定理》一、面试考题试讲题目1.题目:勾股定理2.内容:3.基本要求:(1)试讲时间10分钟;(2)讲解要目的明确、条理清楚、重点突出;(3)根据讲解的需要适当板书;(4)学生掌握勾股定理的证明方法。答辩题目1.勾股定理还有哪些证明方法?2.本节课的设计思路是什么?注:图片节选自人民教育出版社初中数学八年级下册第23-24页
一、考题回顾题目来源:1月6日上午河南省安阳市面试考题试讲题目:初中数学《勾股定理》3基本要求:(1) 要有板书;(2) 试讲十分钟左右;(3) 条理清晰,重点突出;(4 )学生掌握勾股定理的证明方法。答辩题目1.勾股定理的教学过程中,体现了什么数学思想?2.常见的三组勾股数是什么?
名词解释题直角定理逆定理