归纳总结摩尔-库仑强度理论,可以表述为如下要点:()。 A. 当法向应力不很大时,抗剪强度可以简化为法向应力的线性函数,即表示为库伦公式B.将摩尔-库仑强度理论推广于塑性应变理论,即假定屈服条件也不变中主应力的影响,具有这种性质的材料称为摩尔-库仑材料C.剪切破裂面上,材料的抗剪强度是法向应力的函数D.土单元体中,任何一个面上的剪应力大于该面上土体的抗剪强度,土单元体即发生剪切破坏,可用摩尔-库伦破坏准则表示
图示点的应力状态,第三强度理论校核该点的强度条件是(),第四强度理论校核该点的强度条件是()。
图所示点的应力状态,已知材料的许用正应力[σ],其第三强度理论的强度条件是 ()。
图示圆轴,在自由端圆周边界承受竖直向下的集中力F,按第三强度理论,危险截面的相当应力σeq3为:
从结构构件中不同点取出的应力单元体如图所示,构件材料为Q235钢材,若以第三强度理论校核时,则相当应力最大者为( )。A.B.C.D.
如图所示的应力状态单元体若按第四强度理论进行强度计算,则其相当应力σr4等于:
图示直径为d的圆轴,承受轴向拉力F和扭矩T。按第三强度理论,截面危险的相当应力σeq3为( )。
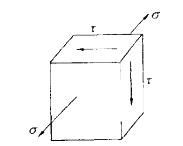
已知图示单元体上的σ>τ,则按第三强度理论其强度条件为:
图示圆轴截面积为A,抗弯截面系数为W,若同时受到扭矩T、弯矩M和轴向力FN的作用,按第三强度理论,下面的强度条件表达式中正确的是( )。
图示钢制竖直杆DB与水平杆AC刚接于B,A端固定,P、l、a与圆截面杆直径d为已知。按第三强度理论,相当应力σr3为:
图示圆轴,在自由端圆周边界承受竖直向下的集中F,按第三强度理论,危险截面的相当应力σeq3为:
图所示单元体的应力状态按第四强度理论,其相当应力σr4为: A.3σ/2B.2σC.7vσ/2D.5vσ/2
如图5-52所示应力状态,按第三强度理论校核,强度条件为( )。
按第三强度理论计算如图5-58所示单元体的相当应力是( )MPa。 A. 20 B. 30 C. 60 D. 50
JB4732-1995《钢制压力容器—分析设计标准》采用的强度理论是()。A第一强度理论B第二强度理论C第三强度理论D第四强度理论
内压圆筒强度计算基本公式的理论依据是()A、第一强度理论;B、第四强度理论C、第三强度理论
认为材料发生脆性断裂的主要因素是最大伸长线应变的强度理论是()。A、第一强度理论B、第二强度理论C、第三强度理论D、第四强度理论
第()强度理论认为,塑性材料屈服破坏的主要原因是最大切应力。A、第一强度理论B、第二强度理论C、第三强度理论D、第四强度理论
圆轴横截面上的扭矩为T,按强度条件算得直径为d,若该横截面上的扭矩变为0.5T,则按强度条件可算得相应的直径0.5d。
我国压力容器设计所采用的强度理论为()。A、第一强度理论B、第二强度理论C、第三强度理论D、第四强度理论
下列强度理论中,考虑了材料抗拉和抗压强度不相等的情况是()A、第一和第二强度理论B、第四强度理论C、第三强度理论D、莫尔强度理论
单选题内压圆筒强度计算基本公式的理论依据是()A第一强度理论;B第四强度理论C第三强度理论
单选题我国压力容器设计所采用的强度理论为()。A第一强度理论B第二强度理论C第三强度理论D第四强度理论
单选题GB 150是以()为设计准则的。A第一强度理论B第二强度理论C第三强度理论D第四强度理论
单选题已知某岩石单轴抗压强度为160MPa,根据格里菲斯理论估算其单轴抗拉强度为()。A10.0MPaB16.0MPaC20.0MPaD25.0MPa
单选题图5-9所示单元体的第三强度理论的相当应力σ r3为()。A 20MPaB 10MPaC 30MPaD 15MPa
单选题塑性材料宜采用()来进行强度分析。A第一第二强度理论B第一第三强度理论C第三第四强度理论D第二第四强度理论
单选题JB4732-1995《钢制压力容器—分析设计标准》采用的强度理论是()。A第一强度理论B第二强度理论C第三强度理论D第四强度理论