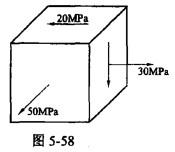
按第三强度理论计算如图5-58所示单元体的相当应力是（ ）MPa。 A. 20 B. 30 C. 60 D. 50
按第三强度理论计算如图5-58所示单元体的相当应力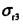
是（ ）MPa。
A. 20 B. 30 C. 60 D. 50
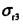是（ ）MPa。
A. 20 B. 30 C. 60 D. 50
参考解析
解析：提示：先将单元体上的应力转换为主应力再代入第三强度理论计算公式得到。
相关考题：
槽形截面梁尺寸及受力图如图所示，AB=3m，BC=1m，z轴为截面形心轴，Iz=1.73×10^8mm4，q=15kN/m。材料许用压应力[σc]=160MPa，许用拉应力[σt]=80MPa。试求：①画梁的剪力图、弯矩图。②按正应力强度条件校核梁的强度。
铸铁T梁的载荷及横截面尺寸如图所示，C为截面形心。已知Iz=60125000mm4，yC=157.5mm，材料许用压应力[σc]=160MPa，许用拉应力[σt]=40MPa。试求：①画梁的剪力图、弯矩图。②按正应力强度条件校核梁的强度。
单元体的应力状态如图所示，则其三个主应力和最大剪应力为（ ）。A．σ1=80MPa，σ2=60MPa，σ3=0，tan=40MPaB．σ1=60MPa，σ2=0，σ3=-80MPa，tan=70MPaC．σ1=-80MPa，σ2=0，σ3=60MPa，tan=-70MPaD．σ1=60MPa，σ2=-80MPa，σ3=0，tan=60MPa
直径为d的圆轴两端承受转矩m的作用而产生扭转变形，材料的泊松比为ν，其危险点的第一强度理论的相当应力σeq1=（），第二强度理论的相当应力σeq2=（），第三强度理论的相当应力σeq3=（）。
单选题图5-9所示单元体的第三强度理论的相当应力σ r3为（）。A 20MPaB 10MPaC 30MPaD 15MPa