若内的可导奇函数,则( )。A、是(一1,1)内的偶函数B、是(一1,1)内的奇函数C、是(一1,1)内的非奇非偶函数D、可能是奇函数,也可能是偶函数
若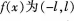 内的可导奇函数,则
内的可导奇函数,则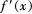 ( )。
( )。
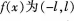 内的可导奇函数,则
内的可导奇函数,则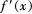 ( )。
( )。A、是(一1,1)内的偶函数
B、是(一1,1)内的奇函数
C、是(一1,1)内的非奇非偶函数
D、可能是奇函数,也可能是偶函数
B、是(一1,1)内的奇函数
C、是(一1,1)内的非奇非偶函数
D、可能是奇函数,也可能是偶函数
参考解析
解析: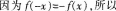
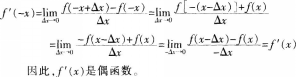
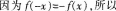
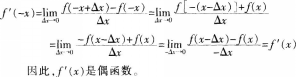
相关考题:
若函数y=f(x)满足条件(63),则在(a,B)内至少存在一点c(a<c<B),使得f′(C)=(f(B)-f(A))/(b-A)成立。A.在(a,B)内连续B.在(a,B)内可导;C.在(a,B)内连续,在(a,B)内可导;D.在[a,B]内连续,在(a,B)内可导。
(3)命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是(A)若f(x) 是偶函数,则f(-x)是偶函数(B)若f(x)不是奇函数,则f(-x)不是奇函数(C)若f(-x)是奇函数,则f(x)是奇函数(D)若f(-x)不是奇函数,则f(x)不是奇函数
(Ⅰ)证明拉格朗日中值定理:若函数f(x)在[a,b]上连续,在(a,b)内可导,则存在ξ∈(a,b),使得f(b)-f(a)=f'(ξ)(b-a);(Ⅱ)证明:若函数f(x)在x=0处连续,在(0,δ)(δ>0)内可导,且=A,则存在,且.
命题“若f(x)为奇函数,则f(-x)为奇函数”的否命题( )。A.若f(x)为偶函数,则f(-x)为偶函数B.若f(x)不是奇函数,则f(-x)不是奇函数C.若f(-x)为奇函数,则fD.若f(-x)为奇函数,则f(x)不是奇函数
单选题若f(x)是在(-l,l)(l>1)内的不恒为0的可导奇函数,则f′(x)( )。A必为(-l,l)内的奇函数B必为(-l,l)内的偶函数C必为(-l,l)内的非奇非偶函数D可能是奇函数也可能是偶函数