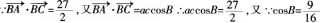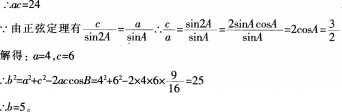若a>b>c>0,且a+b+c=1,求(1)2abc的极大值;(2)a×b×c=1,求2a+b+4c的极小值。
已知图所示电路中,Is=6A,Z0=(6+j8)Ω,Z1=(10+j10)Ω。1)求负载Z的最佳匹配值。2)求在最佳匹配值时负载的功率。
已知三角函数值,用计算器求锐角A,B。(1)sinA=0.6275,sinB=0.0547;(2)cosA=0.6252,cosB=0.1659;(3) tanA=0.8816,tanB=15.94 。
在Rt△ABC中,∠ C=90°,BC=5,sinA=0.7,求cosA,tanA的值。
在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=(2b+c)sinB+(2c+b)sinC.(Ⅰ)求A的大小;(Ⅱ)若sinB+sinC=1,试判断△ABC的形状.
已知△ABC的周长是24cm,三边a、b、c满足c+a=2b,c-a=4cm,求a、b、c的长.
设函数(x)=ax3+bx2+x在x=1处取得极大值5.①求常数a和b;②求函数(x)的极小值.
已知x=-1是函数(x)=ax3+bx2的驻点,且曲线y=(x)过点(1,5),求a,b的值.
已知曲线y=ax3+bx2+cx在点(1,2)处有水平切线,且原点为该曲线的拐点,求a,b,c的值,并写出此曲线的方程.
如图,在Rt△ABC中,∠C=90o,AC=6,BC=8,动点P由起点A沿边AB向终点B运动,每秒2个单位,动点Q由起点B沿边BC向终点C运动,每秒1个单位,P、Q两点同时由起点开始运动,记运动时间为t秒。 (1)设△BPQ的面积为S,求S的最大值: (2)当△BPQ与△ABC相似时,求t的值。
在△ABC中,三个内角A,B,C所对的边分别为a,b,c,已知(1/2)sin2A=sinB?sinC。 (1)若a=2b,求tanC的值;(4分) (2)若A=π/3,b=1,且b
如图,平面四边形ABCD中,AB=2,BC=4,CD=5,DA=3, (1)若∠B与∠D互补,求AC2的值; (2)求平面四边形ABCD面积的最大值。
设A为三阶实对称矩阵,A的每行元素之和为5,AX=0有非零解且λ1=2是A的特征值, 对应特征向量为(-1,0,1)^T. (1)求A的其他特征值与特征向量; (2)求A.
设A是三阶实对称矩阵,r(A)=1,A^2-3A=O,设(1,1,-1)t为A的非零特征值对应的特征向量.(1)求A的特征值;(2)求矩阵A.
设矩阵A= (1)已知A的一个特征值为3,试求y; (2)求可逆矩阵P,使(AP)^T(AP)为对角矩阵.
已知 πΔ2=3.14,πΔ4=3.14161,求[(6/11Δ3)×1/3]Δ4的值。A.0.182B.0.1817C.0.1816D.0.183
在△ABC中,已知∠A=60°,且BC=4AB,求sinC(精确到0.001)。
设实对称阵A的特征值为0,2,2,且对应特征值2的两个特征向量为与,求.
已知直线/:ax+y=1在矩阵对应的变换作用下变为直线Z:x+by=l (1)求实数a,b的值; (2)若点P(x。,yo)在直线Z求点P的坐标。
已知(1)若a//b,求a·b; (2)若a、b的夹角为60。,求la+bl; (3)若a-b与a垂直,求当k为何值时,(ka-b)垂直(a+2b)。
已知数列{an}的前n项和是Sn,且2Sn+an=1(n∈N*)。 (1)求证:数列{an}是等比数列; (2)记bn=10+log9an,求{bn}的前n项和Tn的最大值及相应的n值。
在Excel中,函数AVERAGE(A1:B5)相当于()。A、求(A1:B5)区域的最小值B、求(A1:B5)区域的平均值C、求(A1:B5)区域的最大值D、求(A1:B5)区域的总和
已知1LNaOH溶液中含NaOH0.4g,求溶液的PH值。
在excel 2010的分类汇总功能中,最常用的是对分类数据求()。A、求和B、求最大值C、求平均值D、求最小值
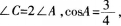
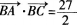 时,求a,b,c的值。
时,求a,b,c的值。 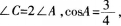
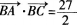 时,求a,b,c的值。
时,求a,b,c的值。 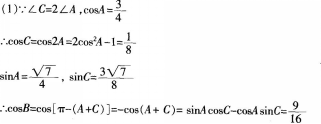 (2)
(2) 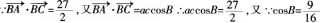
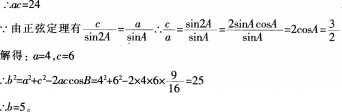
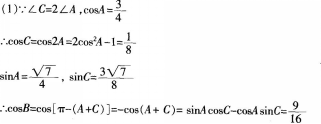 (2)
(2)