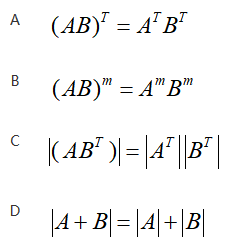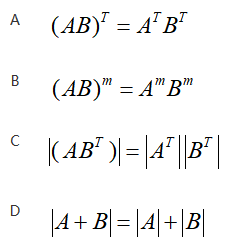某大型整数矩阵用二维整数组 G[1:2M ,l:2N]表示,其中M和N是较大的整数,而且每行从左到右都己是递增排序,每到从上到下也都己是递增排序。元素G[M,N]将该矩阵划分为四个子矩阵A[1:M,1:N],B[1:M,(N+1):2N],C[(M+1):2M,1:N ],D[(M+1):2M,(N+1):2N]。如果某个整数E大于A[M,N],则E( )。A.只可能在子矩阵A中B.只可能在子矩阵B或C中C.只可能在子矩阵B、C或D中D.只可能在子矩阵D中
设A和B均为n阶矩阵,则必有( )。A.|A+B|=|A|+|B|B.AB=BAC.|AB|=|BA|D.
设A为n阶可逆矩阵,则(-A)的伴随矩阵(-A)*等于( )。A.-A.*B.A.*C.(-1)nA.*D.(-1)n-1A.*
设A为m×n阶矩阵,B为n×m阶矩阵,且m>n,令r(AB)=r,则().A.r>mB.r=mC.rD.r≥m
设A为m×n矩阵,C是n阶可逆矩阵,矩阵A的秩为r1,矩阵B=AC的秩为r,则
设A,B,C均为n阶矩阵,E为n阶单位矩阵,若B=E+AB,C=A+CA,则B-C=A.EB.-EC.AD.-A
设A、B均为n阶非零矩阵,且AB=0,则R(A),R(B)满足:A.必有一个等于0B.都小于nC. 一个小于n,一个等于nD.都等于n
设A、B均为n阶非零矩阵,且AB=0,则R(A),R(B)满足:A.必有一个等于0 B.都小于nC. 一个小于n,一个等于n D.都等于n
设A1,A2分别为m阶,n阶可逆矩阵,分块矩阵.证明:A可逆,且
设A是m阶矩阵,B是n阶矩阵,A.- A B B. A B C. (-1)m+n A B D. (-1)mn A B
若M、N均为n阶矩阵,则必有( )。A、|M+N|=|M|+|N|B、|MN|=|NM|C、(MN)′=M′N′D、(M+N)2=M2+2MN+N2
设A为n阶可逆矩阵,则(-A)的伴随矩阵(-A)n等于( )。A. -An B. An C. (-1)nAn D. (-1)n-1An
设A,N,A+B,A-1+B-1均为n阶可逆矩阵,则(A-1+B-1)=()。A、A-1+B-1B、A+BC、C.A(A+-1BD、D.(A+-1
设A为n阶可逆矩阵,则(-A)的伴随矩阵(-A)*等于()。A、-A*B、A*C、(-1)nA*D、(-1)n-1A*
设A,B均为n阶非零矩阵,且AB=0,则RA,RB满足()。A、必有一个等于0B、都小于nC、一个小于n,一个等于nD、都等于n
问答题设A是n阶矩阵,且满足Am=E,其中m为整数,E为n阶单位矩阵。令将A中的元素aij换成它的代数余子式Aij而成的矩阵为A(~),证明:(A(~))m=E。
单选题设A是m×n矩阵,C是n阶可逆矩阵,矩阵A的秩为r,矩阵B=AC的秩为r1,则( )。Ar>r1Br<r1Cr=r1Dr与r1的关系依C而定
单选题设A为n阶方阵,若对任意n×m(m≥n)矩阵B都有AB=0,则A=( )。A0B1C2D3
单选题设A是m×n矩阵,B是n×m矩阵,则( )。A当m>n时,必有|AB|≠0B当m>n时,必有|AB|=0C当n>m时,必有|AB|≠0D当n>m时,必有|AB|=0
填空题设A为n阶方阵,若对任意n×m(m≥n)矩阵B都有AB=0,则A=____.
单选题设A是m×n矩阵,C是n阶可逆矩阵,矩阵A的秩为r,矩阵B=AC的秩为r1,则( )。Ar>r1Br<rlCr=rlDr与r1的关系依C而定
单选题设A为n阶可逆矩阵,则(-A)的伴随矩阵(-A)*等于()。A-A*BA*C(-1)nA*D(-1)n-1A*