在区间[0,1]中随机抽取两个数(χ,y),即(χ,y)服从[0,1]上的均匀分布。求这两个数之差的绝对值小于1/2的概率。
在区间[0,1]中随机抽取两个数(χ,y),即(χ,y)服从[0,1]上的均匀分布。求这两个数之差的绝对值小于1/2的概率。
参考解析
解析:
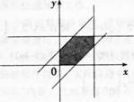


相关考题:
现实世界中随机性多于确定性。在计算机上模拟随机的实际问题,并进行统计计算,这是非常有用的方法。为此,各种程序设计语言都有产生(伪)随机数的函数。这种函数,每调用一次,就可以获得一个位于区间(0,1)内的数。在程序运行时,多次产生的这些数会均匀地分布在0,1之间。在区间(0,1)内均匀分布的含义是指:任取N个随机数,当N足够大时,(56)。应用人员可以利用这种随机数来生成满足指定概率分布的数据,并利用这些数据来模拟实际问题。某程序每获得一对随机数(x,y),都判断x2+y2≤1是否成立。如果N对随机数中,有m对满足这个不等式,则当N足够大时,数值m/N将会比较接近(57)。A.必然有一半数小于1/2,有一半数大于1/2B.大致顺序、等间隔地排列于(0,1)之间C.其中落在任意子区间(a,b)中的数的比率大致接近于b-aD.从小到大排序后,各个数都分别位于(0,1)的Ⅳ等分子区间内
设随机变量X与Y相互独立,且X服从标准正态分布N(0,1),Y的概率分布为P{Y=0}=P{Y=1}=.记Fz(z)为随机变量Z=XY的分布函数,则函数Fz(z)的间断点个数为 A.A0B.1C.2D.3
已知二维随机变量(X,Y)服从区域[0,1]×[0,1]上的均匀分布,则( )。A.P{X>0.5}=0.25B.P{Y>0.5}=0.25C.P{max(X,Y)>0.5}=0.25D.P{min(X,Y)>0.5}=0.25
问答题设随机变景X与Y相互独立,且X服从[0,1]上的均匀分布,y服从λ=1的指数分布, 求:(1)X与Y的联合分布函数. (2)X与y的联合概率密度函数. (3)P{X≥Y}.