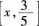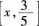设X~N(0,1),Y~N(0,1),且X与Y相互独立,则X+Y服从的分布为() A、X+Y服从N(0,1)B、X+Y不服从正态分布C、X+Y~X2(2)D、X+Y也服从正态分布
在射靶试验中,以是否射中目标为随机事件,并以1表示射中目标,0表示没有射中目标,则射靶两次,其样本空间是________。A.Ω={(1,0)}B.Ω={(1,0),(0,1)}C.Ω={(1,1),(0,0)}D.Ω={(0,0),(0,1),(1,0),(1,1)}
设随机变量X服从正态分布N(0,1),对给定的α(0μα}=α,若P{|X|
设f(x)在闭区间[0,1]上连续,在(0,1)内可导,且f(0)=0,
一根长度为1的细棒位于x轴的区间[0,1]上,若其线密度,则该细棒的质心坐标=
设随机变量X服从参数为2的指数分布,证明:Y=1-在区间(0,1)上服从均匀分布.
设随机变量X在区间(0,1)内服从均匀分布,在X=x(0 (Ⅰ)随机变量X和Y的联合概率密度; (Ⅱ)Y的概率密度; (Ⅲ)概率P{X+Y>1}.
设函数f(x)在区间[0,1]上具有2阶导数,且,证明: (Ⅰ)方程f(x)=0在区间(0,1)内至少存在一个实根; (Ⅱ)方程在区间(0,1)内至少存在两个不同实根.
若随机变量X与Y相互独立,且X在区间[0,2]上服从均匀分布,Y服从参数为3的指数分布,则数学期望E(XY)等于:
在区间[0,1]中随机抽取两个数(χ,y),即(χ,y)服从[0,1]上的均匀分布。求这两个数之差的绝对值小于1/2的概率。
在区间[0,1]内随机取出两个数,则这两个数的平方和也在区间[0,1]内的概率是()。A. 1/2 B.3/4C.π/4 D.1/4
已知函数 (1)求f(x)单调区间与值域; (2)设a≥1,函数g(x)=x3-3a2x-2a,x∈[0,1]。若对于任意x1∈[0,1],总存在x0∈[0,1]使g(x0)=f(x1)成立,求a的取值范围。
(1)若a>0,则?(x)的定义域是__________;(2)若?(x)在区间(0,1]上是减函数,则实数a的取值范围是__________.
随机变量的分布函数的值域是()A、开区间(0,1)B、半开半闭区间(0,1]C、闭区间[0,1]D、半开半闭区间[0,1)
设随机变量X与Y相互独立且都服从区间[0,1]上的均匀分布,则下列随机变量中服从均匀分布的有()。A、X2B、X+YC、(X,Y)D、X-Y
X,Y相互独立,且都服[0,1]上的均匀分布,则服从均匀分布的是().A、(X,Y)B、XYC、X+YD、X-Y
在区间(0,1)内随机地取两个数,则所取两数之和不超过5.0概率为()。
设随机变量X,Y都服从区间[0,1]上的均匀分布,则E(X+Y)=()A、1/6B、1/2C、1D、2
设随机变量X,Y相互独立,且均服从[0,1]上的均匀分布,则服从均匀分布的是()。A、XYB、(X,Y)C、X—YD、X+Y
设X在[0,1]上服从均匀分布,Y=2X+1,则下列结论正确的是()A、Y在[0,1]上服从均匀分布B、Y在[1,3]上服从均匀分布C、Y在[0,3]上服从均匀分布D、P{0≤Y≤1}=1
设X,Y相互独立,且都服从标准正态分布N(0,1),令Z=X2+Y2则Z服从的分布是().A、N(0,2)分布B、单位圆上的均匀分布C、参数为1的瑞利分布D、N(0,1)分布
单选题向区间(0,2)内投点,点落入区间(0,1)内属于( ).A必然事件B不可能事件C随机事件 D无法确定
问答题设函数f(x)在闭区间[0,1]上可微,对于[0,1]上的每一个x,函数f(x)的值都在开区间(0,1)内,且f′(x)≠1,证明在(0,1)内有且仅有一个x,使得f(x)=x。
问答题总体X在[0,1]上服从均匀分布,x1,x2,…,x8为其样本,,则____.
单选题函数y=x2-lnx2的单调减区间是( )。A(-∞,-ln2),(0,ln2)B(-∞,-1),(0,ln2)C(-∞,-ln2),(0,1)D(-∞,-1),(0,1)
单选题甲、乙两射手各进行一次射击,甲射中目标的概率为0.6,乙射中目标的概率为0.5,则至少有一人射目标的概率是()。A0.30B0.50C0.80D其它
单选题设X~N(0,1),则X2服从().Aχ2(n)Bχ2(1)Ct(1)DN(0,1)