浙江省舟山市2022年中考数学试卷(含答案)
一、单项选择题(本大题共30小题,每小题1分,共30分)
在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。错选、多选或未选均无分。
1.清代由盛转衰的时期是( )
A.乾隆朝后期 B.道光朝后期
C.同治帝时期 D.光绪帝时期
单项选择题
第31-50小题,每小题1分。共20分。下列每题给出的四个选项中,只有一个选项是符合题目要求的。请在答题卡上将所选项的字母涂黑。
公民因意外事故下落不明,从事故发生之日起满______,才能符合宣告死亡的条件。
A.1年
B.2年
C.3年
D.4年
解析:我国民法通则第23条规定:“公民有下列情形之一的,利害关系人可以向人民法院申请宣告他死亡:(一)下落不明满四年的;(二)因意外事故下落不明,从事故发生之日起满二年的。战争期间下落不明的,下落不明的时间从战争结束之日起计算。”
【题目描述】
第4题:
正确答案:A
一、选择题(
每小题4分,共40
1.下列是一元一次不等式的是( )
A. B. C. D.
无
选择题(共5题,每题1分,满分5分)
1. Log
A.ロツダB. ロヅツクC. ログD. ロツク
浙江省舟山浙江省舟山市市 2022 年中考数学年中考数学试试卷卷一、一、选择题选择题(本本题题有有 10 小小题题,每,每题题 3 分,共分,共 30 分分)1.若收入 3 元记为+3,则支出 2 元记为()A1B-1C22.如图是由四个相同的小立方体搭成的几何体,它的主视图是()D-2ABCD3.根据有关部门测算,2022 年春节假期 7 天,全国国内旅游出游 251000000 人次,数据 251000000用科学记数法表示为()A2.51108B2.51107C25.1107D0.2511094.用尺规作一个角的角平分线,下列作法中错误的是()ABCD5估计6的值在()A4 和 5 之间B3 和 4 之间C2 和 3 之间D1 和 2 之间6.如图,在ABC 中,AB=AC=8点 E、F、G 分别在边 AB、BC、AC 上EFAC、GFAB、则 四边形 AEFG 的周长是()A32B24C16D87.A、B 两名射击运动员进行了相同次数的射击下列关于他们射击成绩的平均数和方差的描述 中,能说明 A 成绩较好且更稳定的是()A 且 2 2B 且 22C 2D 0,x0)的图象上,点 B 的坐标为(4,3),AB 与 y 轴平行,若 AB=BC,则 k=15某动物园利用杠杆原理称象;如图,在点 P 处挂一根质地均匀且足够长的钢梁(呈水平状态),将装有大象的铁笼和弹簧秤(秤的重力忽略不许)分别悬挂在钢梁的点 A、B 处,当钢梁保持水平时,弹 簧秤读数为 k(N),若铁笼固定不动,移动弹簧秤使 BP 扩大到原来的 n(n1)倍,且钢梁保持水平,则弹簧秤读数为(N)(用含 n,k 的代数式表示)16如图,在扇形 AOB 中,点 C,D 在 上,将 沿弦 CD 折叠后恰好与 OA,OB 相切于点E,F。已知AOB=120,OA=6,则 E 的度数为;折痕 CD 的长为。三、解答三、解答题题(本本题题有有 8 小小题题,第第 1719 题题每每题题 6 分,分,第第 20、21 题题每每题题 8 分,分,第第 22、23 题题每每题题 10 分,第分,第 24 题题 12 分,共分,共 66 分分17(1)计算:38(31)0(2)解不等式:x+84x-118小惠自编一题:“如图在四边形 ABCD 中对角线 AC、BD;交于点 O,ACBD,OB=OD。求 证:四边形 ABCD 是菱形”,并将自己的证明过程与同学小洁交流。小惠:小洁:证明:ACBD,OB=OD,这个题目还缺少条件,需要补充一个条件才能证明。AC 垂直平分 BDAB=AD,CB=CD四边形 ABCD 是菱形若赞同小惠的证法,请在第一个方框内打“”;若赞成小洁的说法,请你补充一个条件,并证明19观察下面的等式:1=1+1,1=1+1,1=1+1,236341245201按上面的规律归纳出一个一般的结论(用含 n 的等式表示,n 为正整数)2请运用分式的有关知识,推理说明这个结论是正确的。206 月 13 日,某港口的湖水商度 y(cm)和时间 x(h)的部分数据及函数图象如下:x(b)1112131415161718y(cm)18913710380101133202260(数据来自某海举研究所)1数学活动:根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象观察函数图象,当 x=4 时,y 的值为多少?当 y 的值最大时,x 的值为多少?2数学思考:请结合函数图象,写出该函数的两条性质或结论3数学应用:根据研究,当潮水高度超过 260cm 时,货轮能够安全进出该港口请问当天什么时间段适合货轮 进出此港口?21小华将一张纸对折后做成的纸飞机如图 1,纸飞机机尾的横截面是一个轴对称图形,其示意图如 图 2,已知 AD=BE=10cm,CD=CE=5cm,ADCD,BECE,DCE=40(1)连结 DE,求线段 DE 的长(2)求点 A、B 之间的距离(结果精确到 0.1cm参考数据:sin200.34,cos200.94,tan200.36sin400.64cos400.77,tan400.84)22.某教育部门为了解本地区中小学生参加家庭劳动时间的情况,随机抽取该地区 1200 名中小学生 进行问卷调查,并将调查向卷(部分)和结果描述如下:中小学生每周参加家庭劳动时间 x(h)分为 5 组:第一组(0 x0.5),第二组(0.5x1),第三组(1x1.5),第四组(1.5x0)个单位得到抛物线 L2,若抛物线 L2 的顶点关于坐标原点 O 的 对称点在抛物线 L1 上,求 m 的值3把抛物线 L1 向右平移 n(n0)个单位得到抛物线 L3,已知点 P(8-t,s),Q(t-4,r)都在抛物线 L3 上,若当 t6 时,都有 sr,求 n 的取值范围24.如图 1,在正方形 ABCD 中,点 F,H 分别在边 AD,AB 上,连结 AC,FH 交于点 E,已知 CF=CH1线段 AC 与 FH 垂直吗?请说明理由2如图 2,过点 A,H,F 的圆交 CF 于点 P,连结 PH 交 AC 于点 K求证:H=H(3)如图 3,在(2)的条件下,当点 K 是线段 AC 的中点时,求的值答案解析部答案解析部分分1.【答案】D2.【答案】B3.【答案】A4.【答案】D5.【答案】C6.【答案】C7.【答案】B8.【答案】A9.【答案】D10.【答案】B11.【答案】m(m+1)12.【答案】1351 3【答案】2514【答案】321 5【答案】1 6【答案】60;4 617【答案】(1)解:原式=2-1=1.(2)解:x+84x-1,3x9,x3.1 8【答案】解:赞成小洁的说法,补充的条件为 AB=CB(或 AD=DC),证明如下:ACBD,OB=OD,AC 垂直平分 BD,AB=AD,CB=CD,AB=CB,AB=AD=CB=CD,四边形 ABCD 为菱形.1 9【答案】(1)解:1=1+1=1+1,2362+12(2+1)1=1+1=1+1,34123+13(3+1)1=1+1=1+1,45204+14(4+1)1=1+1.+1(+1)(2)证明:1+1=+1=+1=1,+1(+1)(+1)(+1)(+1)1=1+1,这个结论是正确的.+1(+1)20【答案】(1)解:依据表中数据,通过描点、连线的方式补全该函数图象如下;由中图象可知,当 x=4 时,y=200;当 y 的值最大时,即图象的最高点,此时对应的 x=21.2解:x=14 时,y 有最小值为 80;当 14x21 时,y 随 x 的增大而增大.3解:当潮水高度超过 260cm 时,货轮能够安全进出该港口,如图所示,当 5x10 和 18x23 时,货轮能够安全进出该港口.2 1【答案】(1)解:如图 2,过点 C 作 CFDE 于点 F,CD=CE=5cm,DCE=40,2DCF=ECF=20,DF=EF=1DE,5在 RtDFC 中,sin20=0.34,DF=1.7cm,DE=2DF=3.4cm.(2)解:如图 2,连接 AB,过点 D 作 DGAB 于点 G,过点 E 作 EHAB 于点 H,AGD=90,由题意可得:CF 垂直平分 AB,DGCF,GDC=DCF=20,又ADCD,A+ADG=GDC+ADG=90,A=GDC=20,10在 RtAGD 中,AD=10cm,cos20=0.94,AG=9.4,同理可得:HB=9.4,AB=AG+GH+HB=AG+DE+HB=9.4+3.4+9.4=22.2cm.答:点 A、B 之间的距离为 22.2cm.2 2【答案】(1)解:总数据个数为 1200,最中间的两个数据是第 600 和第 601 个数据,由统计表可知:前两组的数据个数之和=308+295=603,600 和第 601 个数据均在第二组,中小学生每周参加家庭动时间的中位数落在第二组.2解:每周参加家庭劳动时间大于等于 2 小时的人数有 200 人,每周参加家庭劳动时间不足 2 小时,选择“不喜欢”的人数=(1200-200)(1-43.2%-30.6%-8.7%)=175 人.3解:该地区中小学生大部分学生参加家庭劳动时间少于 2 小时,主要原因为没有时间及家长不 舍得;建议:每天完成作业后,家长要求学生合理参加家庭劳动,并进行指导;学校可开展各种劳动技能社团或课程,鼓励学生积极参加.2 3【答案】(1)解:y=a(x+1)2-4(a0)经过点 A(1,0),0=a22-4,a=1,y=(x+1)2-4.2解:将 L1 的图象向上平移了 m 个单位得到 L2,设 L2 的解析式为 y=(x+1)2-4+m,顶点坐标为(-1,m-4),L2 的顶点关于原点 O 的对称点在 L1 的图象上,(1,4-m)在 L1 的图象上,4-m=(1+1)2-4,m=4.3解:将抛物线 L1 的图象向右平移了 n 个单位得到 L3,设 L3 的解析式为 y=(x+1-n)2-4,抛物线开口向上,对称轴为 x=n-1,P(8-t,s),Q(t-4,r)都在抛物线 L3 上,当 t6 时,都有 sr,P 点在 Q 点左侧,且 sr,当对称轴在 P、Q 之间时,(8-t+t-4)2n-1,n3;当对称轴在点 Q 右侧时,y 随 x 的增大而减小,n-1t-4,nt-3,t6,n3;当对称轴在 P 点的左侧时,y 随 x 的增大而增大,此时 sr,不满足题意,总数所述,当 t6 时,都有 sr,n3.2 4【答案】(1)解:线段 AC 与 FH 垂直,理由如下:正方形 ABCD,B=D=90,CB=CD,BCA=DCA=45,CF=CH,RtCBHRtCDF(HL),BCH=DCF,HCA=FCA,ACFH.(2)解:如图 2,过点 K 作 KMAB 于点 M,AMK=KMH=90=B,MKBC,AMKABC,AK:AC=MK:BC,四边形 AFPH 为圆内接四边形,PHA=DFC,又DFC=BHC,PHA=BHC,即KHM=BHC,HMKHBC,KH:CH=KM:CB,由和得:KH:CH=AK:AC,即 H=.H(3)解:如图 3,H由(2)结论可得:H=,HMKHBC,k 为 AC 中点,H=1,H2MH:BH=1:2,设 MH=m,则 BH=2m,KM=1BC=1AB,AM=MB=1AB,222KM=AM=MB=3m,AH=4m,BC=AB=6m,FH=4 2m,2CH=CF=(2)2+(6)2=210m,EH=1AH=2 2m,FAH=90,FPH=90,又PFH=EHC,PFHEHC,PF:EH=FH:HC,即 PF:2 2m=4 2m:210m,5PF=410m,CP=CF-PF=210m-410m=610m,55610541032=5=.
有一份选择题试卷共6个小题,其得分标准是:一道小题答对得8分,答错得0分,不答得2分,某位同学得了20分,则他( )。
A.至少答对一道题 B.至少有三个小题没答
C.至少答对三个小题
D.答错两个小题
设答对数为x,答错数为y,不答数为z,则:
8x+0y+2z=20。
A选项表示x=1,那么得出z>6,不正确。
B选项表示z可能为3,4,5,将3,4,5代入式中全不正确。
C选项表示x可能为3,4,5,代入式中也全不正确。
D选项表示y=2,代入式中与题所述并不抵触,表示很有可能,故选D。
【题目描述】
第20题:
【题目描述】
一、单项选择题(本大题共20小题,每小题2分,共40分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。错选、多选或未选均无分。
1.构成微机系统CPU的两部分是 ( )
A.EU和BIU
B.ALU和BIU
C.ALU和EU
D.存储器和运算器

已知,得分至少为3分的,人均2x分;得分最多为7分的,人均x分。这个班级总人数是:
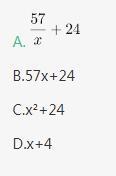
第二步,设得分至少为3分的人数为y,则全班总分数=2x×y+2×5+1×3=2xy+13①;得分至少为7分的人数为y+5+3+8-2-2-4=y+8,则全班总分数=(y+8)×x+2×10+2×9+4×8=xy+8x+70②。根据①=②,化简可得xy=8x+57,则

因此,选择A选项。

已知,得分至少为3分的,人均2x分;得分最多为7分的,人均x分。这个班级总人数是:
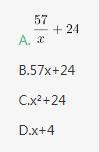
第二步,设得分至少为3分的人数为y,则全班总分数=2x×y+2×5+1×3=2xy+13①;得分最多为7分的人数为y+5+3+8-2-2-4=y+8,则全班总分数=(y+8)×x+2×10+2×9+4×8=xy+8x+70②。根据①=②,化简可得xy=8x+57,则

因此,选择A选项。
相关考题:
- 非应计贷款是指贷款本金或利息逾期 90 天没有收回的贷款。
- 关于马斯洛的需要层次理论的说法,错误的是( ). A.未被满足的需要是行为的主要激励源 B。获得基本满足的需要具有强的激励作用 C。基本需要主要靠内部条件满足,高级需要主要靠外在条件满足 D.管理者在进行激励时,需要考虑每个员工的特殊需要以及占主导地位的需要层次 E。组织用于满足员工的低层次需要的投入效益是递减的
- 下面哪个概念不属于社会学习理论( )。A.观察学习B.自我效能C.自我实现D.替代学习
- ( 难度:中等)Hive有哪些方式保存元数据A.derbyB.MySQLC.hdfsD.SQLite
- 2020年以中国为主要贸易伙伴的国家,已经超过百分之多少
- ( 难度:中等)下列关于Hadoop API的说法正确的是A.Hadoop的文件API不是通用的,只用于HDFS文件系统B.Configuration类的默认实例化方法是以HDFS系统的资源配置为基础的C.FileStatus对象存储文件和目录的元数据D.FSDataInputStream是javio.DataInputStream的子类
- ( 难度:中等)Flume的数据源支持哪些A.KafkaB.HTTPC.ThriftD.Avro
- ( )是我们后天慢慢习得的一种社会规范和道德,亦即被内化的道德。A.自我B.超我C.本我D.自性
- 银行账务组织包括哪些内容?各项内容之间的关系如何?
- 关于成就需要的说法,错误的是( )。 A.成就需要是指个体追求优越感的驱动力 B.成就需要高的人倾向选择适度的风险 C.成就需要高的人具有较强的责任心和进取意识 D.一般来说,成就需要高的人工作绩效较低