勾股定理同步测试题
设关系R和s的元数分别为2和3,那么,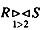 与(20)等价。设关系 P和Q具有相同的关系模式,所列出的等价式中(21)是不正确的。设关系模式R(ABC)上成立的FD集为{A→B1,p1={AB,B,C)为R的一个分解,那么,p1(22);若R(ABC)上成立的FD集为{A→C,B→C),p2={AB,AC}为R的一个分解,那么,分解P2(23);若R(ABC)上成立的FD集为{B→ C),p3={AB,BC}为R的一个分解,那么,p3(24)。
与(20)等价。设关系 P和Q具有相同的关系模式,所列出的等价式中(21)是不正确的。设关系模式R(ABC)上成立的FD集为{A→B1,p1={AB,B,C)为R的一个分解,那么,p1(22);若R(ABC)上成立的FD集为{A→C,B→C),p2={AB,AC}为R的一个分解,那么,分解P2(23);若R(ABC)上成立的FD集为{B→ C),p3={AB,BC}为R的一个分解,那么,p3(24)。
A.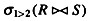
B.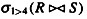
C.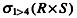
D.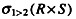
⊿ABC中,∠ABC、∠ACB的平分线相交于点O。
(1)若∠ABC = 40°,∠ACB = 50°,则∠BOC = 。
(2)若∠ABC +∠ACB =116°,则∠BOC = 。
(3)若∠A = 76°,则∠BOC = 。
(4)若∠BOC = 120°,则∠A = 。
(5)你能找出∠A与∠BOC 之间的数量关系吗?
(1)135°;(2)122°;(3)128°;(4)60°;(5)∠BOC = 90°+
A.欧几里得定理 B.勾股定理
C.阿基米德定律 D.黄金分割率
 的值?
的值?
B.503000
C.2012
D.20120


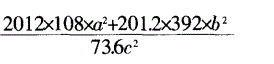 的值?
的值?
B.503000
C.2012
D.20120

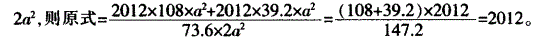
PAGE PAGE 3勾股定理课堂学习检测一、填空题1如果直角三角形的两直角边长分别为a、b,斜边长为c,那么_c2;这一定理在我国被称为_2ABC中,C90,a、b、c分别是A、B、C的对边(1)若a5,b12,则c_;(2)若c41,a40,则b_;(3)若A30,a1,则c_,b_;(4)若A45,a1,则b_,c_3如图是由边长为1m的正方形地砖铺设的地面示意图,小明沿图中所示的折线从ABC所走的路程为_4等腰直角三角形的斜边为10,则腰长为_,斜边上的高为_5在直角三角形中,一条直角边为11cm,另两边是两个连续自然数,则此直角三角形的周长为_二、选择题6RtABC中,斜边BC2,则AB2AC2BC2的值为( )(A)8(B)4(C)6(D)无法计算7如图,ABC中,ABAC10,BD是AC边上的高线,DC2,则BD等于( )(A)4(B)6(C)8(D)8如图,RtABC中,C90,若AB15cm,则正方形ADEC和正方形BCFG的面积和为( )(A)150cm2(B)200cm2(C)225cm2(D)无法计算三、解答题9在RtABC中,C90,A、B、C的对边分别为a、b、c(1)若ab34,c75cm,求a、b;(2)若ac1517,b24,求ABC的面积;(3)若ca4,b16,求a、c;(4)若A30,c24,求c边上的高hc;(5)若a、b、c为连续整数,求abc综合、运用、诊断一、选择题10若直角三角形的三边长分别为2,4,x,则x的值可能有( )(A)1个(B)2个(C)3个(D)4个二、填空题11如图,直线l经过正方形ABCD的顶点B,点A、C到直线l的距离分别是1、2,则正方形的边长是_12在直线上依次摆着7个正方形(如图),已知倾斜放置的3个正方形的面积分别为1,2,3,水平放置的4个正方形的面积是S1,S2,S3,S4,则S1S2S3S4_三、解答题13如图,RtABC中,C90,A30,BD是ABC的平分线,AD20,求BC的长拓展、探究、思考14如图,ABC中,C90(1)以直角三角形的三边为边向形外作等边三角形(如图),探究S1S2与S3的关系;图(2)以直角三角形的三边为斜边向形外作等腰直角三角形(如图),探究S1S2与S3的关系;图(3)以直角三角形的三边为直径向形外作半圆(如图),探究S1S2与S3的关系图
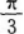 【考情点拨】本题主要考查的知识点为余弦定理.
【考情点拨】本题主要考查的知识点为余弦定理.
【应试指导】
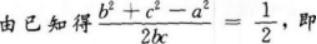
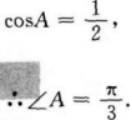


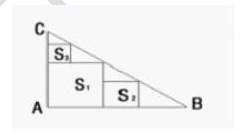
B.a2=b2+c2
C.a2=2b2+2c2
D.a3=b3+c3
E.a3=2b3+2c3
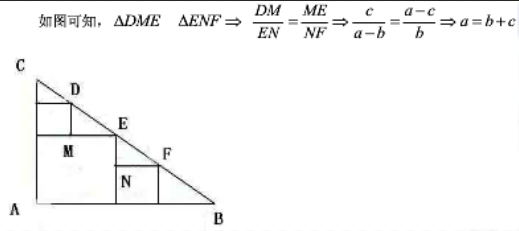
A.欧几里得定理 B.勾股定理
C.阿基米德定律 D.黄金分割率
 的三条边分别是a,b,C,且a2+b2=c2。证明:ΔABC是直角三角形。(这是勾股定理的逆命题)
的三条边分别是a,b,C,且a2+b2=c2。证明:ΔABC是直角三角形。(这是勾股定理的逆命题) 

全等.故ABC是直角三角形。
相关考题:
- 单选题恶性淋巴瘤( )。ABCDE
- 《伊利亚特》描写的是特洛亚战争。全部情节围绕着一个主要人物、一个事件展开。这就是()。
- 单选题血红蛋白电泳( )。ABCDE
- 学术批评要坚持学术与学术对话,不同学术观点的争议要采用()的方法来进行。A、公开发表学术批评文章B、学术评价C、据理力争D、召开学术会议
- 公司制的核心是建立所有者和经营者相互制衡的()。A、体制B、机制C、关系D、结构
- 在莫泊桑著名的小说《羊脂球》中,马车上的乘客包括()A、妓女、卖酒商人、参议员、伯爵B、妓女、参议员、高利贷者、伯爵C、妓女、卖酒商人、参议员、律师D、妓女、卖酒商人、普鲁士军官、伯爵
- 单选题下列哪组产物是由交联后纤维蛋白的降解产生的?( )AX、Y、D、E及D-二聚体BX’、Y’、D、E及A、B、C、H碎片CX、Y、D、E及A、B、C、H碎片DX、Y、D、E和A、B、C、H碎片及D-二聚体EX’、Y’、E’及D-二聚体
- 单选题该患者病情符合的诊断是( )。A恶性贫血B缺铁性贫血C白细胞不增加性白血病D粒细胞减少症E再生障碍性贫血
- 开创俄国“自然派”的作家是()A、冈察洛夫B、克雷洛夫C、果戈理D、别林斯基
- 单选题正常骨髓象特征包括( )。A原淋+幼淋占10%BM:E为5:1C幼红细胞约占有核细胞的20%D原粒+早幼粒占9%E颗粒型巨核细胞数为35%