20212022学年苏科版八年级数学上册第一章全等三角形单元测试卷【含答案】
从平面A外一点P P引与A相交的直线,使得P点与交点的距离等于1,则满足条件的直线条数一定不可能是:
A、0条 B、1条 C、2条 D、无数条
如图所示,点P为正方形ABCD内一点,且PA=1,PB=2,PC=3试求∠ABP的度数?
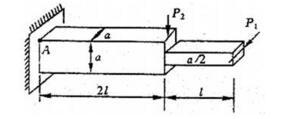
已知P1=12,P2=10,距离OA=1O,OB=8.66,OC=4.36,AB=5,AC=9,则合力对A点的力矩为( )。
A.140
B.150
C.160
D.170
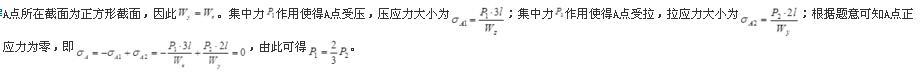
(苏科版)八年级数学上册第一章 全等三角形 单元测试卷一、单选题1如图,点P是AOB平分线OC上一点,PDOB,垂足为D,若PD=2,则点P到边OA的距离是( )A2B3CD42如图,CEBF,CE=BF,则添加下列条件还不能使EACFDB,()AAB=CDBAEDFCE=FDAE=DF3如图,ABCDEF,DF和AC,FE和CB是对应边若A100,F46,则DEF等于()A100B54C46D344如图所示,已知平分,若,则等于( )ABCD5如图所示,ABBD,ACCD,D=35,则A的度数为()A65B35C55D456如图,AC=BC,垂足分别是点D、E若AD=6,BE=2,则DE的长是( )A2B3C4D57如图是用直尺和圆规作一个角等于已知角,那么能得出的依据是运用全等三角形判定( )A边边边B边角边C角边角D角角边8下列说法正确的是()A全等三角形是指形状相同大小相等的三角形B全等三角形是指面积相等的三角形C周长相等的三角形是全等三角形D所有的等边三角形都是全等三角形二、填空题9如图,若D为BC中点,那么用“SSS”判定ABDACD需添加的一个条件是 _10如图, 是的中位线, 是的中点,射线与交于点,与的延长线交于点下列结论:; ;,正确的有_(填序号)11在ABC中,AB=AC,点DE在BC上,连接AD、AE,如果只添加一个条件使DABEAC,则添加的条件为_(只填写一种情况即可)12如图,在ABC中,ABC和ACB的平分线相交于点O,过点O作EFBC,分别交AB、AC于点E、F若AB8,AC5,那么AEF的周长为_13如图,点B、E、C、F在一条直线上,ABDE,BE=CF,请添加一个条件_,使ABCDEF14如图,在ABC中,已知AD=DE,AB=BE,A=80,则CED=_度15如图所示,在ABC中, AD平分BAC,点E在DA的延长线上,且EFBC,且交BC延长线于点F,H为DC上的一点,且BH=EF, AH=DF, AB=DE,若DAC+nACB90,则_三、 解答题16如图,已知直角,线段m,利用尺规作直角三角形ABC,使C90,ACm,BC2m.不写作法,但要保留作图痕迹17 如图,ABC中,AB=AC,D是BC的中点,试说明ADBC18如图,已知,两条对应边在同一条直线上,连结交于点,若=3,则图中阴影部分面积为_19已知:如图,点O在BAC的平分线上,BOAC,COAB,垂足分别为D,E.求证:OBOC20已知:如图,正方形ABCD,E,F分别为DC,BC中点求证:AE=AF21如图,在中,于,于,是上一点,是延长线一点,连接,(1)求证:;(2)探求线段,有什么关系,并证明22如图,已知CF90,ACDF,AEDB,BC与EF交于点O,(1)求证:RtABCRtDEF;(2)若A51,求BOF的度数23(2016.镇江)如图,AD、BC相交于点O,AD=BC,C=D=90(1)若ABC=35,求CAO的度数;(2)求证:CO=DO24如图,已知,点、在线段上(1)线段与的数量关系是:_,判断该关系的数学根据是: (用文字表达);(2)判断与之间的位置关系,并说明理由25已知:如图,点 A、B、C、D 在一条直线上,ACDB,AEDF,BECF求证:ABEDCF.26小明和小亮在学习探索三角形全等时,碰到如下一题:如图1,若AC=AD,BC=BD,则ACB与ADB有怎样的关系?(1)请你帮他们解答,并说明理由(2)细心的小明在解答的过程中,发现如果在AB上任取一点E,连接CE、DE,则有CE=DE,你知道为什么吗?(如图2)(3)小亮在小明说出理由后,提出如果在AB的延长线上任取一点P,也有第2题类似的结论请你帮他画出图形,并证明结论答案1A作PEOA于E,点P是AOB平分线OC上一点,PDOB,PEOA,PE=PD=2,故选A2DCEBF,ACB=DBF.A.AB=CD,AC=DB,又ACB=DBF,CE=BF,EACFDB(SAS),故A不符合题意;B.AEDF,A=D,又ACB=DBF,CE=BF,EACFDB(AAS),故B不符合题意;C. ACB=DBF,E=F,CE=BF,EACFDB(AAS),故C不符合题意;D.当AE=DF时,不能使EACFDB故选D3DABCDEF,DA100,DEF180DF34,故选D4D平分,DOC=BOC,DCO=BOC,DOC=DCO,CD=OD=4cm,故选:D.5B解:ABBD,ACCD,B=C=90,A+AEB=D+CED=90又AEB=CED,A=D=35故选B6C,ACD+ECB=90,ADC=CEB=90,ECB+CBE=90,ACD=CBE,在ACD和CBE中,ADC=CEB=90,ACD=CBE,AC=BC,ACDCBE(AAS),AD=CE=6,CD=BE=2,ED=EC-CD=6-2=4故选择:C7A由作图可知OD=OD=OC=OC,CD=CD,ODCODC(SSS),AOB=AOB,故选A.8A根据全等三角形的定义,能够完全重合的三角形是全等三角形,故选A9AB=AC添加AB=AC,D为BC的中点,BD=CD,在ABD和ACD中,ABDACD(SSS),故AB=AC10解:是的中位线,是的中点,又,,错误 又,由两式相减,得正确 正确 连接设,可得其他三角形面积如图,错误故11BD=CE(或BE=CD或AD=AE或BAD=EAC或BDA=AEC或ADE=AED或BAE=DAC)由AB=AC可得B=C,(1)要证DABEAC可直接添加的一个条件是:BD=CE(由“SAS”可证全等)或ADB=AEC(由“AAS”可证全等)或BAD=CAE(由“ASA”可证全等);(2)添加条件:BE=CD可证得BD=CE;(3)添加条件:BAE=CAD可证得BAD=CAE;(4)添加条件:ADE=AED看证得ADB=AEC;(5)添加条件:AD=AE可证得ADE=AEC;综上所述,若只添加一个条件证DABEAC,共有如上7种添加方法,直接3种,间接4种.1213解:由ABC与ACB的平分线相交于点O,得EBO=OBC,FCO=OCB由EF/BC,得EOB=BOC,FOC=OCB,EOB=EBO,FOC=FCO,EO=BE,OF=FCCAEF=AE+EF+AF=AE+BE+AF+CF=AB+AC=8+5=13故1313AB=DE(答案不唯一)BE=CF,BC=EF.ABDE,B=DEF.在ABC和DEF中,已有一边一角对应相等.添加AB=DE,可由SAS证明ABCDEF;添加BCA=F,可由ASA证明ABCDEF;添加A=D,可由AAS证明ABCDEF;等等.14100在ABD和EBD中 ,ABDEBD(SSS),A=DEB,A=80,CED=18080=100故答案为100.15解:在RtABH和RtDEF中,RtABHRtDEF(HL),EDF=BAH,EDF-BAD=BAH-BAD,B=DAH,AD平分BAC,BAD=DAC,设B=DAH=y,BAD=DAC=x,2y+x=90,CAH=DAC-DAH=x-y,ACB=90-CAH =3y,DAC+nACB=90,x+3ny=90,3n=2,n=,故16见解析解:作出的ABC如图所示17详见解析D是BC的中点BD=CD在ABD和ACD中,BD=CD,AB=AC,AC=ACADBADCADB=ADC,ADB+ADC=1800,ADB=ADC=900,ADBC189,AB=DC,ABC=DCE,AB/DCABP=CDP,在ABP和CDP中ABPCDPBP=DP,阴影部分面积为3+6=9故919见解析点O在BAC的平分线上,BOAC,COAB,OE=OD,BEO=CDO=90,在BEO和CDO中,BEOCDO(ASA),OB=OC20详见解析 四边形ABCD为正方形, AB=AD,B=D=90,DC=CB E、F为DC、BC中点, DE=DC,BF=BC DE=BF 在ADE和ABF中,AD=ABD=BDE=BF,ADEABF(SAS) AE=AF21(1)证明见解析;(2)AGAF,AG=AF,证明见解析解:(1)于,于,ADB=AEC=90,ABD+BAD=90,ACE+BAD=90,(2)结论:AF=AG,AFAG理由如下:在ABF和GCA中,ABFGCA(SAS),AF=AG,GAC=AFB,AFB=ADB+FAD,GAC=GAF+FAD,GAF=ADF,ADF=90,GAF=90,AGAF,AG
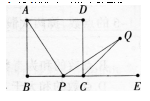

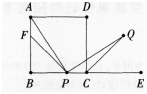
∴AP=PQ。

(1)求证:AB为圆的直径;
(2)若AC=BD,AB=5,求弦DE的长。

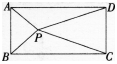
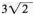
解析:矩形内的点到相对顶点的距离平方和相等,即PA2+PC2=PB2+PD2,即32+52=42+PD2,
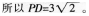
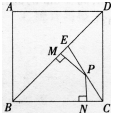
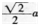
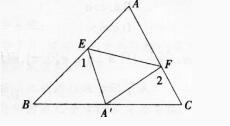
解析:作EK⊥BC于K,连接BP,由△EBC的面积等于△PBE和△PBC的面积之和且BE=
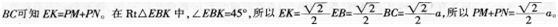
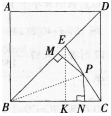
相关考题:
- 多选题下列哪一种激素不是肾脏产生的非血管活性物质()A肾素B缓激肽释放酶CPGE2DEPOEPGF2a
- 出汗可降低体温,排除内热,祛风解毒。下列蔬菜具有发汗功能的是()A、葱B、菠菜C、大白菜D、西瓜
- 电气工程图的幅面尺寸分六类,为A0~A5。
- 单选题女,36岁,因突发寒战、高热、腰痛、尿急、尿频、尿痛入院。既往无类似病史。查:体温39.4℃,右侧肾区有叩击痛;尿比重1.020,尿蛋白+,白细胞+++,白细胞管型0~2个/HP。该病人最可能的诊断是()A急性肾小球肾炎B慢性肾小球肾炎C急性肾盂肾炎D慢性肾盂肾炎E膀胱炎
- 多选题女性,25岁,因颜面部皮疹、双下肢水肿2年,尿量减少2周入院。查体:BP150/90mmHg,颜面部斑丘疹呈蝶翼样分布,双下肢可凹性水肿。提问:下列哪项是狼疮活动的指标()A明显血尿B急性肾衰竭C大量蛋白尿DC3下降E抗ds-DNA抗体(+)F血沉快
- 单选题血浆清除率是0的是()A尿素B葡萄糖C菊粉D碘E蛋白质
- 消防泵启动线路,采用消火栓按钮箱中常开触点串联接法,可靠性好。
- 主动型红外报警器是由()组成,是一种红外线光束,截断型报警器。A、发射器B、传感器C、接受器D、感应器E、处理器
- 变压器的差动保护可以保护变压器的短路事故。
- 参照代号