某构件受力简图如图,则点O的力矩Mo为()。A、P.aB、P.bC、P.cD、P.d
某构件受力简图如图,则点O的力矩Mo为()。
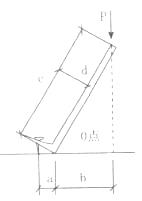

A、P.a
B、P.b
C、P.c
D、P.d
B、P.b
C、P.c
D、P.d
参考解析
解析:2017版教材P10页原文是使物体绕某点转动的效果要用力矩来度量 。 “ 力矩 == 力 力臂” , 即转动中心称力矩中心 , 力臂是力矩中心 O 点至力 P 的作用线的垂直距离 , 见图 1A411022- 1 。
相关考题:
某外伸梁如图所示,F=qa/2,M=2qa2。已知q、a画受力图如图(b)所示。其中,均布载荷q简化为作用于D点的一个集中力FQ,FA、FBy和为三个待求的未知。由∑Fx=0可得:FBx=(\t)。A.qaB.2qaC.3qaD.O
某厂房的围护结构设有悬吊式墙架柱,墙架柱支承于吊车梁的辅助桁架上,其顶端采用弹簧板与屋盖系统相连,底端采用开椭圆孔的普通螺栓与基础相连,计算简图如图2-7所示。钢材采用Q235钢,墙架柱选用热轧H型钢HM244x175x7x11,截面形式如图2-7所示,其截面特性:A=55.49x102mm2,Wx=495x1O3mm3。试问,在围护结构自重和水平风荷载的共同作用下,AB段和 BC段墙架柱的受力状态应为下列何项所示?(A) AB段和BC段墙架柱均为拉弯构件(B) AB段和BC段墙架柱均为压弯构件(C) AB段墙架柱为拉弯构件,BC段墙架柱为压弯构件(D) AB段墙架柱为压弯构件,BC段墙架柱为拉弯构件
某轴心受拉构件的受力情况和截面尺寸如图所示,承受的静力荷载设计值为N=1000kN,钢材为Q235A,构件截面无削弱,则截面所能承受的最大横向荷载设计值F(不考虑构件自重)为( )kN。 A、70.3 B、85.3 C、100.56 D、512
某平面任意力系向O点简化后,得到如图4-7所示的一个主矢FR和一个主矩MO, 则该力系的最后简化结果为( )。A.作用在O点的一个合力 B.合力偶C.作用在O点右边某点的一个合力 D.作用在O点左边某点的一个合力
某轴心受拉构件的受力情况和截面尺寸如图所示,承受的静力荷载设计值为N=1000kN,钢材为Q235A,构件截面无削弱,则截面所能承受的最大横向荷载设计值F(不考虑构件自重)为( )kN。 A.70.3 B.85.3 C.100.56 D.512
若已知力F对直角坐标系原点O的力矩矢的大小∣MO(F)∣,方向沿Oy向,则此力对此坐标系中各轴的矩为()。A、Mx(F)=0, My(F)=0,Mz(F)=0B、Mx(F)=0,M y(F)= ∣MO(F)∣,Mz(F) =∣MO (F)∣C、Mx(F)=0,My(F)= ∣MO(F)∣,MZ(F)=0D、Mx(F)=0,My(F)=0, Mz(F)= ∣MO(F)∣
平面任意力系的主矢为R´,力系对于任一点的主矩为MO,则该力系平衡的充分和必要条件是:()。A、R´=0,MO=0B、R´≠0,MO=0C、R´=0,MO≠0D、R´≠0,MO≠0