1.矩形的判定(含答案)

在平行四边形ABCD中，∠DAB＝60°，AB＝15cm．已知⊙O的半径等于3cm，AB，AD分别与⊙O相切于点E，F，⊙O在平行四边形ABCD内沿AB方向滚动，与BC边相切时运动停止，试求⊙O滚过的路程．

正确答案：
解：

平行四边形中，已知AB、BC及其夹角∠ B（∠ B是锐角），能求出平行四边形ABCD的面积S吗？如果能，写出用AB，BC及其夹角∠ B表示S的式子。

S=BC×AB×sinB

在平行四边形ABCD中，∠DAB=60，AB=15cm，已知圆O的半径等于3cm，AB，AD分别与圆O相切于点E，F.圆0在平行四边形ABCD内沿AB方向滚动，与BC边相切时运动停止．试求圆O滚过的路程．

答案：

解析：

若顺次连接四边形ABCD各边中点所得四边形是矩形，则四边形ABCD一定是( )。

A.对角线相互垂直的四边形
B.矩形
C.对角线相等的四边形
D.菱形

答案：A

解析：

对角线相互垂直的四边形顺次连接各边中点所得四边形是矩形，对角线相等的四边形顺次连接各边中点所得四边形是菱形。

如图，已知一个四边形中边AD长为3cm，边BC长7cm；∠DAB＝135°，∠ABC=∠ADC=90°那么这个四边形的面积是（）cm2。

答案：D

解析：

第一步，本题考查几何问题，用割补平移法解题。
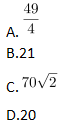
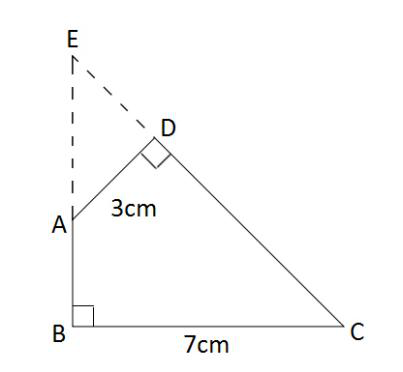
第二步，作BA和CD的延长线交于E，如图所示，得到三角形EBC和ADE。容易知道所求四边形ABCD面积等于△EBC面积减去△ADE面积。由题意∠DAB＝135°，∠ABC＝∠ADC＝90°，可以求得∠DCB＝360°－135°－90°×2＝45°，且∠BEC＝∠EAD＝45°，所以△EBC和△ADE都是等腰直角三角形。
第三步，因为AD长3cm，BC长7cm，则BE＝BC＝7cm，DE＝AD＝3cm，所以

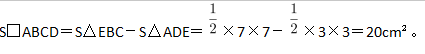
摘要:矩形的判定ABCD1.如图所示，在四边形中，已知AB∥DC，AB=DC，在不添加任何辅助线的前提下，要想该四边形为矩形，只需加上的一个条件是（填上你认为正确的一个答案即可）．2.如图，已知四边形中，∠A=∠C=90∘，且ABCDAD=BC，求证：四边形ABCD是矩形．3.如图，在平行四边形∠AOB=¿ABCD中，对角线时，平行四边形AC，BDABCD交于点O，AB=OA，则当是矩形．4.下列命题中，不正确的是()A．有三个角是直角的四边形是矩形B．四个角都相等的四边形是矩形C．有一个角是直角的平行四边形是矩形D．对角线互相平分的四边形是矩形5.已知：如图，在平行四边形ABCD求证：平行四边形ABCD6.如图，在DE交△ABCBC于点中，对角线AC，BDO，∠1=∠2．相交于点是矩形．中，AB=BC，BD平分∠ABC．四边形F，连接CE．求证：四边形BECDABED是矩形．是平行四边形，7.已知：如图，平行四边形ABCD各角的平分线分别相交于点E、F、G、H．求证：EFGH四边形是矩形．E、F8.如图，已知∘∠AEC=90为平行四边形．求证：四边形ABCDAECF的对角线上的两点，且BE=DF，为矩形．9.如图，将平行四边形ABCD的边AB延长到点E，使BE=AB，DE交边BC于点F.(1)求证：BF=CF;12(2)若∠A=∠EFC，求证：四边形BECD是矩形10.如图，四边形ABCD是平行四边形，AC，BD(1)求证：四边形ABCD是矩形；(2)若∘∠BOC=120，AB=4cm，求四边形11.如图，在△ABC平行四边形ABDE，连接中，AB=AC

如图所示，△ABC是直角形，四边形IBFD和四边形HFGE都是正方形，已知AI=1cm，IB＝4cm，问正方形HFGE的面积是多少（）

答案：C

解析：

C。设正方形HFGE的边长为X，由三角形EHD相似于三角形DIA可知，EH/DH=DI/DA，即X/（X-4）=4/1，解得X=16/5，那么正方形面积为X的平方等于10.24。

如图所示，△ABC是直角形，四边形IBFD和四边形HFGE都是正方形，已知AI=1cm，IB＝4cm，问正方形HFGE的面积是多少（）

答案：C

解析：

C。设正方形HFGE的边长为X，由三角形EHD相似于三角形DIA可知，EH/DH=DI/DA，即X/（X-4）=4/1，解得X=16/5，那么正方形面积为X的平方等于10.24。

如图，已知一个四边形中边AD长为3cm，边BC长7cm；∠DAB＝135°，∠ABC=∠ADC=90°那么这个四边形的面积是（）。

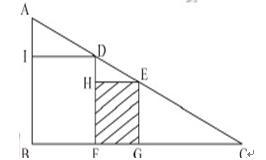
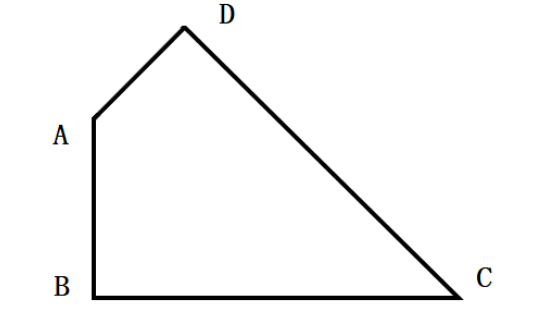
A.49/4
B.21
C.

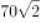
D.20

答案：D

解析：

如图所示，△ABC是直角形，四边形IBFD和四边形HFGE都是正方形，已知AI=1cm，IB＝4cm，问正方形HFGE的面积是多少（）

答案：C

解析：

C。设正方形HFGE的边长为X，由三角形EHD相似于三角形DIA可知，EH/DH=DI/DA，即X/（X-4）=4/1，解得X=16/5，那么正方形面积为X的平方等于10.24。

如图所示，ΔABC是直角三角形，四边形和四边形都是正方形，已知4cm，问正方形HFGF的面积是多少？（）

答案：C

解析：