初中数学升学摸底考试02
一个扇形的圆心角为90°,半径为2,则这个扇形的弧长为________。(结果保留π)
扇形弧长可用公式:求得,由于本题n=90°,r=2,因此这个扇形的弧长为π。
答案:π
涉及知识点:弧长公式
点评:与圆有关的计算一直是中考考查的重要内容,主要考点有:弧长和扇形面积及其应用等。
推荐指数:★★★★
下列平面图形中,即是轴对称图形又是中心对称图形的是( )

A.A
B.B
C.C
D.D

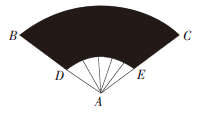
B.(400/3)π
C. 800π
D.(800/3)π
-10^2)=(800/3)π,故本题选D。
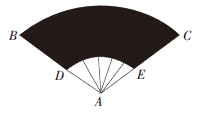
B.(400/3)π
C. 800π
D.(800/3)π
-10^2)=(800/3)π,故本题选D。
编号 02初中数学升学摸底考试试 卷 一、选择题(本题有10小题,每小题4分,共40分请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)1.计算的结果是( )A、 B、 C、 D、32.如右图,由三个小立方体搭成的几何体的俯视图是( )3.二次函数y=x2的图象向上平移2个单位,得到新的图象的二次函数表达式是()A、B、C、D、4.在中,AB=15,sinA=,则BC等于()A、45B、5C、D、5. 下列图形中,既是轴对称图形,又是中心对称图形的是 ()答案在第5页6.某住宅小区六月份中1日至6日每天用水量变化情况如图所示,那么这6天的平均用水量是()A、30吨 B、31吨C、32吨 、33吨7.一个扇形的圆心角是120,它的面积为3cm2,那么这个扇形的半径是()A、cm、3cm、6cm、9cm8.如图,O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是()A、4B、6C、7D、89.根据下列表格的对应值: x 3.233.243.253.260.060.020.030.09判断方程(a0,a,b,c为常数)一个解x的范围是( )A、3x3.23 B、3.23x3.24 C、3.24x3.25 D、3.25 x3.26 10.一个均匀的立方体六个面上分别标有数1,2,3,4,5,6右图是这个立方体表面的展开图抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的的概率是()A、B、C、D、试 卷 请将本卷的答案或解答过程用钢笔或圆珠笔写在答卷上二、填空题(本题有6小题,每小题5分,共30分)11.点P(1,2)关于y轴对称的点的坐标是 12.如图所示,直线ab,则A= 度13.已知O的半径为8, 圆心O到直线l的距离是6, 则直线l与O的位置关系是 14.如果直角三角形的斜边与一条直角边的长分别是13cm和5cm,那么这个直角三角形的面积是 cm215.在日常生活中如取款、上网等都需要密码有一种用“因式分解”法产生的密码,方便记忆原理是:如对于多项式,因式分解的结果是,若取x=9,y=9时,则各个因式的值是:(xy)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码对于多项式,取x=10,y=10时,用上述方法产生的密码是:(写出一个即可)16.两个反比例函数,在第一象限内的图象如图所示, 点P1,P2,P3,P2 005在反比例函数图象上,它们的横坐标分别是x1,x2,x3,x2 005,纵坐标分别是1,3,5,共2 005个连续奇数,过点P1, P2,P3,P2 005分别作y轴的平行线,与的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),Q2 005(x2 005,y2 005),则y2 005= 三、解答题(本题有8小题,第1720题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)17.(1) 计算:-;(2) 解方程:18.如图,在ABCD中,E,F是对角线AC上的两点,且AE=CF求证:BE=DF19.我国政府在农村扶贫工作中取得了显著成效据国家统计局公布的数据表明,2004年末我国农村绝对贫困人口为2 610万人(比上年末减少290万人),其中东部地区为374万人,中部地区为931万人,西部地区为1 305万人请用扇形统计图表示出2004年末这三个地区农村绝对贫困人口分布的比例(要在图中注明各部分所占的比例)20.请将四个全等直角梯形(如图),拼成一个平行四边形,并画出两种不同的拼法示意图(拼出的两个图形只要不全等就认为是不同的拼法)21.一个矩形,两边长分别为xcm和10cm,如果它的周长小于80cm,面积大于100cm2求x的取值范围22.某电脑公司现有A,B,C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑(1) 写出所有选购方案(利用树状图或列表方法表示);(2) 如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?(3) 现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示),恰好用了10万元人民币,其中甲品牌电脑为A型号电脑,求购买的A型号电脑有几台23.据了解,火车票价按“”的方法来确定已知A站至H站总里程数为1 500千米,全程参考价为180元下表是沿途各站至H站的里程数:车站名ABCDEFGH各站至H站的里程数(单位:千米)15001130910622402219720例如,要确定从B站至E站火车票价,其票价为(元)(1) 求A站至F站的火车票价(结果精确到1元);(2) 旅客王大妈乘火车去女儿家,上车过两站后拿着火车票问乘务员:我快到站了吗?乘务员看到王大妈手中票价是66元,马上说下一站就到了请问王大妈是在哪一站下车的?(要求写出解答过程)24.如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上动点D在线段BC上移动(不与B,C重合),连接OD,过点D作DEOD,交边AB于点E,连接OE记CD的长为t(1) 当t时,求直线DE的函数表达式;(2) 如果记梯形COEB的面积为S,那么是否存在S的最大值?若存在,请求出这个最大值及此时t的值;若不存在,请说明理由;(3) 当OD2DE2的算术平方根取最小值时,求点E的坐标参考答案1、 选择题(本题有10小题,每小题4分,共40分)题号12345678910答案AACBDCBDCA题号12345678910答案AACBDCBDCA二、填空题(本题有6小题,每小题5分,共30分)11. (1,2)12. 2213. 相交14. 30 15. 101030,或103010,或30101016.2004.5三、解答题(本题有8小题,第1720题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)17.解:(1) -=(每项算对,各给1分)3分 = 1分(注:用计算器求解正确或只写答案均给3分)(2) 去分母,得5(x+1)=3(x1),分去括号,得5x+5=3x3,分移项、合并同类项,得2x=x=分经检验,x=是原方程的根,所以,x=是原方程的根分18.证法一: 四边形ABCD是平行四边形, ABCD, AB=CD2分
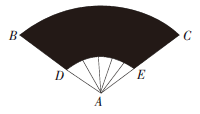
B.(400/3)π
C. 800π
D.(800/3)π
-10^2)=(800/3)π,故本题选D。
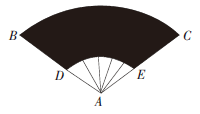
B.(400/3)π
C. 800π
D.(800/3)π
-10^2)=(800/3)π,故本题选D。
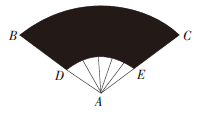
B.(400/3)π
C. 800π
D.(800/3)π
-10^2)=(800/3)π,故本题选D。
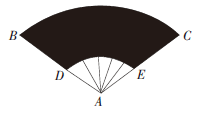
B.(400/3)π
C. 800π
D.(800/3)π
-10^2)=(800/3)π,故本题选D。
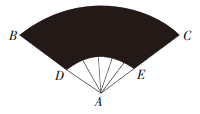
B.(400/3)π
C. 800π
D.(800/3)π
-10^2)=(800/3)π,故本题选D。
相关考题:
- 双母线中任一组电压互感器停役,可不必进行一次倒闸操作,但需按以下要求执行()。A、将接于检修压变上的线路保护切换至另一条母线压变上B、母差保护投互联方式C、母联断路器改“非自动方式”D、需停用母差保护
- 燃料在料床内上下翻滚燃烧的燃烧方式称为()。A、固定燃烧B、悬浮燃烧C、沸腾燃烧D、以上都不对
- 填空题MVB总线传输的三类数据是过程数据、()数据和()数据。
- 翻车事故中,对车辆造成的损坏下列描述错误的是()A、易造成车身整体变形B、车身局部严重损坏C、车辆可判为全损D、翻滚过程中会造成车身侧面损坏
- 医院感染流行病学三大要素是什么?
- 血液透析患者因溶血.透析不充分.单超.进食过多水果蔬菜,最容易发生何种紊乱()A、高钠血症B、低钾血症C、高钾血症D、高磷血症E、低钙血症
- 消毒供应中心应建立持续质量改进及措施,并建立灭菌物品的()A、考核制度B、召回制度C、改进制度D、应急制度
- 下列情况中可以不将重合闸停用的为()。A、空充线路时B、线路有人带电工作C、重合闸装置异常D、断路器遮断容量不足
- 问答题简述过渡段长度公式及公式中字母的含义?
- 单选题接触网耐张零件的机械强度安全系数不应小于()。A2.0B3.0C3.5D4.0
- 2022广东省国家工作人员学法考试系统考试真题(2022年6月1日-7月10日)+题库+100(考场一+考场二+考场三)_
- 2022年广东省学法考试系统考试真题(2022年6月1日-7月10日)+题库+100分(考场一+考场二+考场三)_
- 2022年广东省国家工作人员学法考试系统考试(2022年6月1日-7月10日)真题题库+答案+100分(考场一)_
- (2022年6月1日-7月10日)2022年广东省国家工作人员学法考试系统+专项测试题真题答案+第二板块(100分)_
- 2022年广东省国家工作人员学法考试系统考试真题(2022年6月1日-7月10日)+题库+100分(考场一+考场二+考场三)_
- 2022广东省学法考试系统考试(2022年6月1日-7月10日)真题+题库+答案+100(考场一)_
- (2022年6月1日-7月10日)2022广东省学法考试系统专项测试题+真题+答案第一板块(100分)_
- (2022年6月1日-7月10日)2022年广东省学法考试系统+专项测试题真题答案+第二板块(100分)_
- 2022年广东省学法考试系统考试(2022年6月1日-7月10日)真题+题库+100(考场一+考场二+考场三)_
- 2022年广东省国家工作人员学法考试系统考试(2022年6月1日-7月10日)真题+题库答案100分(考场一)_