初中数学升学摸底考试17

若反比例函数的图象经过点A(-2,1) ,则它的表达式是 _________________ ．

正确答案：

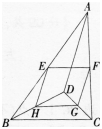
⊿ABC中，∠ABC、∠ACB的平分线相交于点O。

（1）若∠ABC = 40°，∠ACB = 50°，则∠BOC = 。

（2）若∠ABC +∠ACB =116°，则∠BOC = 。

（3）若∠A = 76°，则∠BOC = 。

（4）若∠BOC = 120°，则∠A = 。

（5）你能找出∠A与∠BOC 之间的数量关系吗？

正确答案：
（1）135°；（2）122°；（3）128°；（4）60°；（5）∠BOC = 90°+ ∠A

下列命题中，正确的是( ).

A.单调函数的导函数必定为单调函数
B.设f´(x)为单调函数，则f(x)也为单调函数
C.设f(x)在(a，b)内只有一个驻点xo，则此xo必为f(x)的极值点
D.设f(x)在(a，b)内可导且只有一个极值点xo，f´(xo)=0

答案：D

解析：

可导函数的极值点必定是函数的驻点，故选D.

下列命题中，正确的是( ).

答案：D

解析：

可导函数的极值点必定是函数的驻点，故选D.

如图，已知圆C与x轴相切于点T(1，0)，与y轴正半轴交于两点A，B(B在A的上方)且AB=2，则圆C在点8处的切线在x轴上的截距_________。

答案：

解析：

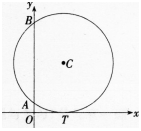
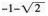
解析：连接BC，CT，设半径为r，由于T为切点，所以CT⊥x轴，点C到AB的距离为1，

编号 17初中数学升学摸底考试一、选择题（本大题有10小题，每小题3分，共30分）13的绝对值是（）A3B3CD2将不等式的解集在数轴上表示出来，应是（）3在O中，弦AB与CD相交于点M，AM4，BM3，则（）A28B21C12D74在一定条件下，若物体运动的路程s（米）与时间t（秒）的关系式为，则当时，该物体所经过的路程为（）A28米B48米C68米D88米5如图，D、E、F分别为ABC三边的中点，则与DEF全等的三角形有（）A1个B2个C3个D5个6下列因式分解中，结果正确的是（）ABCD7在ABC中，D、E分别是AB、AC边上的点，DEBC，ADE30，C120，则A（）A60B45C30D208如图，OP平分AOB，PCOA于C，PDOB于D，则PC与PD的大小关系（）APCPDBPCPDCPCPDD不能确定9如图，反比例函数与直线相交于点A，A点的横坐标为1，则此反比例函数的解析式为（）ABCD10现规定一种新的运算“”：，如，则（）AB8CD答案在第5页二、填空题（本大题有8小题，每小题3分，共24分）11已知月球与地球的距离约为384000km，这个距离用科学计数法表示为_km。12正六边形的一个内角的度数是_13用换元法解方程时，可设y，则原方程可化为_14某移动公司为了调查手机发送短信的情况，在本区域的1000位用户中抽取了10位用户来统计他们某月份发送短信息的条数，结果如下表所示：手机用户序号12345678910发送短信息条数85788379848586888085则本次调查中抽取的样本容量是_，中位数是_，众数是_15如图，是排洪水管的横截面，若此管道的半径为54cm，水面以上部分的弓形弧的弧长为30cm，则这段弓形弧所对的圆心角的度数为_16若一个一元二次方程的解为，则这个方程可以是_（只要求写出一个）。17当x_时，分式有意义18已知：P为O外一点，PA切O于A，过P点作直线与O相交，交点分别为B，C，若PA4，PB2，则BC_三、解答题（本大题共4小题，计28分）19计算20如图，已知，在ABC中，F是AC的中点，E为AB上一点，D为EF延长线上一点，AACD求证：CDAE21先化简后求值：，其中22我边防战士在海拔高度（即CD的长）为50米的小岛顶部D处执行任务，上午8时发现在海面上的A处有一艘船，此时测得该船的俯角为30，该船沿着AC方向航行一段时间后到达B处，又测得该船的俯角为45，求该船在这一段时间内的航程（计算结果保留根号）23求一个一元二次方程，使它的两根为、，且满足，24如图，已知与是等圆，它们相交于A、B两点，在上，AC是的直径，直线CB交于D，E为AB延长线上一点，连结DE。（1）请你连结AD，证明：AD是的直径（2）若E60，求证：DE是的切线25已知：抛物线的解析式为（1）求证：此抛物线与x轴必有两个不同的交点；（2）若此抛物线与直线的一个交点在y轴上，求m的值。26学校书法兴趣小组准备到文具店购买A、B两种类型的毛笔，文具店的销售方法是：一次性购买A型毛笔不超过20支时，按零售价销售；超过20支时，部分超过每支比零售价低0.4元，其余部分仍按零售价销售。一次性购买B型毛笔不超过15支时，按零售价销售；超过15支时，部分超过每支比零售价低0.6元，其余部分仍按零售价销售。（1）如果全组共有20名同学，若每人各买1支A型毛笔和2支B型毛笔，共支付145元；若每人各买2支A型毛笔和1支B型毛笔，共支付129元。这家文具店的A、B两种类型毛笔的零售价各是多少？（2）为了促销，该文具店对A型毛笔除了原来的销售方法外，同时又推出了一种新的销售方法：无论购买多少支，一律按原零售价（即（1）中所求得的A型毛笔的零售价）的90%出售。现要购买A型毛笔a支（a40），在新的销售方法和原销售方法中，应选择哪种方法购买花钱较少？并说明理由。27已知，如图，现有、的正方形纸片和的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）在下面的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使拼出的矩形面积为，并标出此矩形的长和宽。28已知：如图所示，直线l的解析式为，并且与x轴、y轴分别交于点A、B。（1）求A、B两点的坐标；（2）一个圆心在坐标原点、半径为1的圆，以0.4个单位/秒的速度向x轴正方向运动，问在什么时刻与直线l相切；（3）在题（2）中，若在圆开始运动的同时，一动点P从B点出发，沿BA方向以0.5个单位/秒的速度运动，问在整个运动过程中，点P在动圆的圆面（圆上和圆内部）上，一共运动了多长时间？29已知，在矩形ABCD中，AB2，E为BC上一点，沿直线DE将矩形折叠，使C点落在AB边上的C点处，过作CHDC，CH分别交DE、DC于点G、H，连结CG，C C，C C交GE于点F。（1）求证：四边形CG CE为菱形；（2）设，并设，试将y表示成x的函数（3）当（2）中所求得的函数的图象达到最高点时，求BC的长。9

如图,D是△ABC内的一点，BD⊥CD，AD=6，BD=8，CD=6，E，F，G，H分别是AB，AC，CD， BD的中点．则四边形EFGH的周长是()。

A.12
B.14
C.15
D.16

答案：D

解析：

因为BD⊥CD，BD=8，CD=6，由勾股定理可知BC=10。由三角形中位线定理可知EH=FG=

如图所示。直线AB与DF相交于点0，OD平分∠BOC，EO⊥D0，垂足为0，则∠COF与∠BOE的差为()。

A.30o
B.45o
C.60o
D.90o

答案：D

解析：

∠COF+∠COD=180°，∠BOE+∠BOD=90°，且∠COD=∠BOD，两式相减可知∠COF- ∠BOE=90°。

如图，AB是⊙O的直径，AC是弦，直线EF和⊙O相切与点C，AD⊥EF，垂足为D。
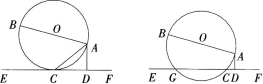
(1)若 ∠DAC=63°，求∠BAC；(5分)
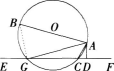
(2)若把直线EF向上平行移动，如图，直线EF交 ⊙O于G和C两点，若题中的其他条件不变，这时与∠DAC相等的角是哪一个为什么 (5分)

答案：

解析：

(1)证明：连接OC，则OC⊥EF，且OC=OA，易得∠OCA=∠OAC。 ∵AD⊥EF，∴OC∥AD。∴∠OCA=∠CAD，∴∠CAD=∠OAC=63°
(2)与∠CAD相等的角是∠BAG。
证明如下：如图，连接BG。∵四边形ACGB是⊙O的内接四边形．
∴∠ABG+∠ACG=180°。
∵D，C，G共线,∴∠ACD+∠ACG=180°。
∴∠ACD=∠ABG。
∵AB是⊙O的直径,∴∠BAG+∠ABG=90°
∵AD⊥EF∴∠CAD+∠ACD=90°∴∠CAD=∠BAG

在等腰直角三角形ABC中，过直角顶点C在∠ACB内部任作一条射线CM，与线段AB交于点M，则AC>AM的概率是______。

答案：

解析：

如图，在梯形ABCD中，AB//CD，O为AC与BD的交点，CO=2AO，则梯形ABCD与三角形AOB的面积之比为：

A.6：1
B.7：1
C.8：1
D.9：1

答案：D

解析：

在梯形中，上底与下底平行，可得△AOB~△COD，其面积之比等于对应边AO、CO之比的平方，为1:4。△AOB与△BOC可看成两个等高的三角形，面积之比等于底AO、CO之比，为1:2。显然△AOD与△BOC面积相等。设△AOB面积为1，则梯形面积为1+2+2+4=9。故所求为9:1。

51题库考试学习网

51tk.com

初中数学升学摸底考试17

相关考题：