求函数的极大值与极小值．
求函数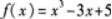
的极大值与极小值．
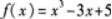的极大值与极小值．参考解析
解析：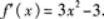
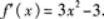
相关考题：
● 某一类应用问题中，需要求正比例函数与反比例函数之和的极值。例如，正比例函数 4x 与反比例函数 9/x 之和用 f(x)表示， 即 f(x)=4x + 9/x， （x0） ,那么函数 f(x) （63） 。（63）A. 没有极小值B. 在 x=1 时达到极大值C. 在 4x=9/x 时达到极小值D. 极大值是极小值的 9/4 倍
设函数f(x)在内连续，其导函数的图形如图所示，则f(x)有(52)。A．一个极小值点和两个极大值点B．两个极小值点和一个极大值点C．两个极小值点和两个极大值点D．三个极小值点和一个极大值点
设f（x）=xsinx+cosx，则下列命题中正确的是（ ）。A.f（0）是极大值，f（π/2）是极小值B.f（0）是极小值，f（π/2）是极大值C.f（0）是极大值，f（π/2）也是极大值D.f（0）是极小值，f（π/2）也是极小值。
f（x）在（－∞，＋∞）内连续，其导数函数f′（x）图形如图所示，则f（x）有（ ）。A．一个极小值点和两个极大值点B．两个极小值点和两个极大值点C．两个极小值点和一个极大值点D．一个极小值点和三个极大值点
设函数y-f(x)连续，除x=a外f''(x)均存在。一一阶导函数y'=f(x)的图形如下，则y=f(x)A.有两个极大值点，一个极小值点，一个拐点B.有一个极大值点，一个极小值点，两个拐点C.有一个极大值点，一个极小值点，一个拐点D.有一个极大值点，两个极小值点，两个拐点
单选题设f（x）＝xsinx＋cosx。下列命题中正确的是（ ）。Af（0）是极大值，f（π/2）是极小值Bf（0）是极小值，f（π/2）是极大值Cf（0）是极大值，f（π/2）也是极大值Df（0）是极小值，f（π/2）也是极小值
单选题解析法是应用（）的原理求目标函数的极大值或极小值，得到设计变量的最优解。A数学规划B最小二乘C相似性D最小二乘和相似性