图8—1是资产组合价值变化△Ⅱ的概率密度函数曲线,其中阴影部分表示( )。 图8—1资产组合价值变化△Ⅱ的概率密度函数曲线A.资产组合价值变化跌破-VaR的概率是1-α%B.资产组合价值变化跌破-VaR的概率是α%C.资产组合价值变化超过-VaR的概率是α%D.资产组合价值变化超过-VaR的概率是1-α%
图8—1是资产组合价值变化△Ⅱ的概率密度函数曲线,其中阴影部分表示( )。
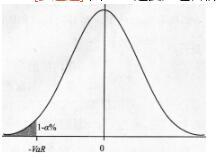
图8—1资产组合价值变化△Ⅱ的概率密度函数曲线

图8—1资产组合价值变化△Ⅱ的概率密度函数曲线
A.资产组合价值变化跌破-VaR的概率是1-α%
B.资产组合价值变化跌破-VaR的概率是α%
C.资产组合价值变化超过-VaR的概率是α%
D.资产组合价值变化超过-VaR的概率是1-α%
B.资产组合价值变化跌破-VaR的概率是α%
C.资产组合价值变化超过-VaR的概率是α%
D.资产组合价值变化超过-VaR的概率是1-α%
参考解析
解析:钟形曲线是资产组合价值变化△Ⅱ的概率密度函数曲线,阴影部分的意思表示资产组合价值变化跌破-VaR的概率是1-“%。由此可以看出,阮R实际上是某个概率分布的分位数。
相关考题:
生产函数Q=f(L,K)的要素组合与产量的对应图,如图所示,这张图是以坐标平面的形式编制的。其中,横轴和纵轴分别表示劳动投入量和资本投入量,虚线交点上的数字表示与该点的要素投入组合对应的产量。(1)图中是否存在规模报酬递增、不变和递减?(2)图中是否存在边际报酬递减?(3)图中哪些要素组合处于同一条等产量曲线上?
关于正态分布N(μ,ó2)的说法,正确的有( )。A.μ是正态分布的均值,描述了密度函数曲线的中心位置B.ó是正态分布的标准差,ó越大,密度函数曲线越平缓C.正态分布概率密度函数曲线中间高,两边低,左右对称D.正态分布是离散随机变量的一种常见分布E.两个正态分布的μ相同时,对应的概率密度曲线重合
图4-1为四条气温年变化曲线,关于该图的描述,正确的是( ) A.①曲线表示巴西亚马孙平原气温变化B.②曲线表示俄罗斯莫斯科的气温变化 C.③曲线表示澳大利亚悉尼的气温变化D.④曲线表示美国纽约的气温变化
某细胞有丝分裂过程中染色体变化如下图。图A中曲线a表示染色体的着丝点与纺锤丝的相应极之间的平均距离:图8中①~⑥表示有丝分裂染色体数目变化曲线;图C中①②③表示上述过程中染色质与染色体的变化。分析回答:(1)图A中,曲线b表示 __________。a曲线距离减小的原因是 __________。(2)从__________分钟后,细胞分裂进入后期,相当于B图曲线 __________段,该细胞染色体数目最多时有 __________条。(3)图C中①~②发生在图B的__________ 阶段,图C中②一③发生在有丝分裂的__________ 期。①和③的相同点是__________ ;①和③的不同点是__________ 。
图8—1是资产组合价值变化△Π的概率密度函数曲线,其中阴影部分表示( )。A.资产组合价值变化跌破-VaR的概率是1-a%B.资产组合价值变化跌破-VaR的概率是a%C.资产组合价值变化超过-VaR的概率是a%D.资产组合价值变化超过-VaR的概率是1-a%
对于一般正态分布,如X~N(1,4),则有关该正态分布的概率密度曲线的叙述不正确的是()。A、该分布的概率密度函数曲线关于x=1对称B、在x=1处达到最大值C、x轴为渐近线D、该概率密度函数曲线关于y轴对称
问答题【背景材料】建设工程风险评价中,常用风险量函数R=f(p,q)来定量衡量(其中,R表示风险量,p表示风险的发生概率,q表示潜在损失),图1-1所示为三条不同的等风险量曲线图。 确定风险等级图(图1-2)中的等级划分。
单选题下面关于t分布的说法,正确的有()。At分布的概率密度函数在整个轴上呈偏态分布Bt分布的概率密度函数在正半轴上呈偏态分布C自由度为n-1的t分布概率密度函数与标准正态分布N(0,1)的概率密度函数的图形大致类似D自由度为n-1的t分布概率密度函数与二项分布b(n,p)的概率密度函数的图形大致类似
单选题正态概率密度函数的值表示的是某一变量出现的()。A概率B次数C概率函数D概率密度