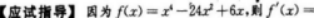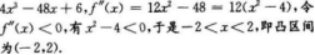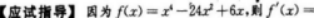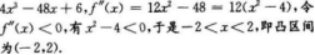设函数f(x)的定义域是(0,1),那么f(x+1)的定义域是()。 A.(0,1)B.(-1,0)C.(1,2)D.(0,2)
若函数y=f(x)是一随机变量的概率密度,则()一定成立。 A、y=f(x)的定义域为[0,1]B、y=f(x)非负C、y=f(x)的值域为[0,1]D、y=f(x)在(-∞,+∞)内连续
已知函数f(x)=x3-4x2.(I)确定函数f(x)在哪个区问是增函数,在哪个区间是减函数;(Ⅱ)求函数f(x)在区间[0,4]上的最大值和最小值.
若定义域关于原点对称,且f(-x)=f(x),则f(x)是奇函数。() 此题为判断题(对,错)。
设定义域在R上的函数f(x)=x|x|,则f(x)是A.奇函数,增函数B.偶函数,增函数C.奇函数,减函数D.偶函数,减函数
f(x)=x-arc cotx,其增减性为( )。A.在(-∞,+∞)内是单调递增B.在定义域内是单调递增C.在(-∞,+∞)内是单调递减D.在定义域内是单调递减
函数:y=sin1/x在定义域内是:A.单调函数 B.周期函数C.无界函数 D.有界函数
函数f(x)=x4-24x2+6x在定义域内的凸区间是()A.(-∞,0)B.(-2,2)C.(0,+∞)D.(-∞,+∞)
如果在区间(a,b)内,函数f(x)满足f′(x)>0,f′′(x)A.单调递增且曲线为凹的B.单调递减且曲线为凸的C.单调递增且曲线为凸的D.单调递减且曲线为凹的
函数f(x)的导函数f'(x)的图像如右图所示,则在(-∞,+∞)内f(x)的单调递增区间是()A.(-∞,0)B.(-∞,1)C.(0,+∞)D.(1,+∞)
如果在区间(a,b)内,函数,(z)满足f’(x)>0,f"(x)A.单调递增且曲线为凹的B.单调递减且曲线为凸的C.单调递增且曲线为凸的D.单调递减且曲线为凹的
A.常数k<-1B.函数f(x)在定义域范围内,y随着x的增大而减小C.若点C(-1,m),点B(2,n),在函数f(x)的图象上,则m<nD.函数f(x)图象对称轴的直线方程是y=x
若实值函数f定义域为全体实数,且满足任意x,y:f(x+y)=f(x)f(y)。此时,若f(8) = 4,则有f(2)=( )。
在定义域内下列函数中为增函数的是( )A.f(x)=2-xB.f(x)=-log2xC.f(x)=x3D.f(x)=x2+1
(本小题13分)已知函数f(x)=2x3-3x2,求(1)函数的单调区间;(2)函数f(x)在区间[-3,2]的最大值与最小值。
下列函数在定义域内,既是奇函数又是增函数的是()A.y=sinx B.y=log2x C.y=x+8D.y=x3
函数y=f(x)在(a,6)内二阶可导,且f′(x)>0,f″(x)<0,则曲线y=f(x)在(a,6)内( ).《》( )A.单调增加且为凹B.单调增加且为凸C.单调减少且为凹D.单调减少且为凸
(1)叙述函数f(x)在区间a,b]中上凸的定义,并证明f(x)=sinx在[0,π]中上凸;(4分) (2)若A、B、C为某三角形的三内角。证明
(1)若a>0,则?(x)的定义域是__________;(2)若?(x)在区间(0,1]上是减函数,则实数a的取值范围是__________.
已知函数f(x)在区间(0,1)内可导,则以下结论正确的是( )。
随机变量X的分布函数F(x)是一个实函数,其定义域是();值域是()。
单选题当a<x<b时,有f′(x)>0,f″(x)<0,则在区间(a,b)内,函数y=f(x)的图形沿x轴正向是( )。[2012年真题]A单调减且凸的B单调减且凹的C单调增且凸的D单调增且凹的
问答题设函数f(x)在闭区间[0,1]上可微,对于[0,1]上的每一个x,函数f(x)的值都在开区间(0,1)内,且f′(x)≠1,证明在(0,1)内有且仅有一个x,使得f(x)=x。
问答题设不恒为常数的函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b)。证明:在(a,b)内至少存在一点ξ,使得f′(ξ)>0。
单选题(2012)当a区间(a,b)内,函数y=f(x)图形沿x轴正向是:()A单调减且凸的B单调减且凹的C单调增且凸的D单调增且凹的
单选题设在区间(-∞,+∞)内函数f(x)>0,且当k为大于0的常数时有f(x+k)=1/f(x)则在区间(-∞,+∞)内函数f(x)是( )。A奇函数B偶函数C周期函数D单调函数
单选题设函数f(x)在区间[1,+∞)内二阶可导,且满足条件f(1)=f′(1)=0,x>1时f″(x)<0,则g(x)=f(x)/x在(1,+∞)内( )。A曲线是向上凹的B曲线是向上凸的C单调减少D单调增加